GraphChi -- Large-Scale Graph Computation on Just a PC

GraphChi: Large-Scale Graph Computation on Just a PC

引言

GraphChi是一个有代表性的单机的Out-of-Core的图计算系统。它的Paper发表在OSDI’12上面。GraphChi为了处理大规模的图，它将图划分为小规模的子图。使用Parallel Sliding Windows(PSW)等的方法来使用基于磁盘的处理方式。GraphChi可以在一台普通的PC上面实现处理大规模的图，

with only fraction of the resources, GraphChi can solve the same problems in very reasonable time. Our work makes large-scale graph computation available to anyone with a modern PC.

基于磁盘的图计算

GraphChi也是采用了常见的以顶点为中心的模型。对于一个顶点为中心的模型，一个实例的代码如下所示：

Update(vertex) begin
  x[] ← read values of in- and out-edges of vertex ; vertex.value ← f(x[]) ;
  foreach edge of vertex do
    edge.value ← g(vertex.value, edge.value); 
  end
end

在Pregel之类的系统中，采用的执行方式是Bulk-Synchronous Parallel(BSP)模型，而在GraphChi中，采用的模型为Parallel Sliding Windows(PSW)。它是一种异步的模型，Paper中认为，这种模型能获得比BSP模型更加好的性能。此外，GraphChi还必须处理下面的问题：

稀疏图格式保存，在GraphChi中，图是被保存到磁盘上面的。以compressed sparserow (CSR)格式保存方便快速load顶点的出边道内存。另外为了能够在以顶点为中心的模型中高效地访问图的入边，GraphChi页使用了compressed sparse column (CSC)的格式保存入边的信息。这样方便顺序范围顶点的相关的入边。这样实际上每条边都会被保存2次；
随机访问的问题，上面的做法并不能保证高兴地去更新边的信息。如果不做处理将会导致大量的随机读写操作，大大降低性能。

Parallel Sliding Windows

Parallel Sliding Windows的计算模型是GraphChi的一个核心，一个基本的示意的伪代码如下：

foreach iteration do
  shards[] ← InitializeShards(P) 
  for interval ← 1 to P do
     /* Load subgraph for interval, using Alg. 3. 
     * Note, that the edge values are stored as pointers to the loaded file blocks. 
     */
    subgraph ← LoadSubgraph (interval) 
    parallel foreach vertex ∈ subgraph.vertex do
      /* Execute user-defined update function, which can modify the values of the edges */
      UDF updateVertex (vertex) /* Update memory-shard to disk */
      shards[interval].UpdateFully()
      /* Update sliding windows on disk */
    end
    s ∈ 1,..,P, s != interval do 
      shards[s].UpdateLastWindowToDisk()
    end 
  end
end

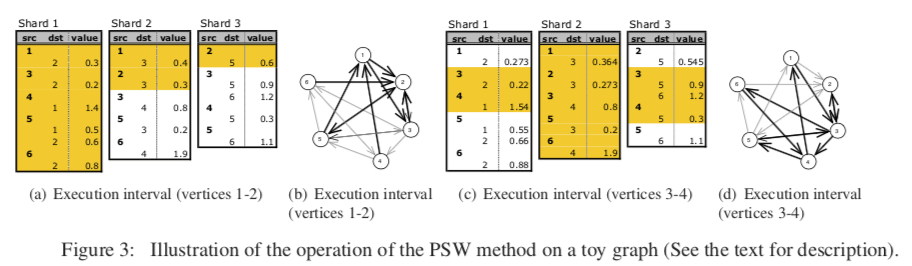
在只需要很少量的随机访问的情况下，PSW就可以更新边的值。基本的操作分为3部分：1 从磁盘中加载子图；2. 更新顶点和边的操作；3. 将更新之后的数据写到磁盘上面；

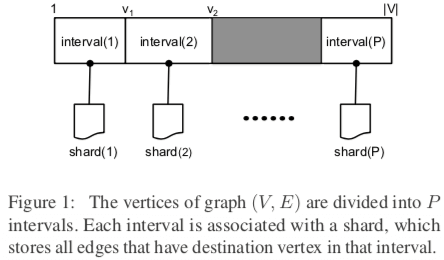
加载子图；一个图G会被分割为不相交的区间，每一个区间会有一个对应的shard的结构，这里面保存的是以这个区间内的顶点为目的顶点的边的集合，并且会根据它们的源顶点来排序。分割图的时候，要考虑到尽量地将它们分割均匀，而且要都能加载到内存里面，不能太大。这里分割考虑的大小主要是根据边，要保证边的数量尽量一致，而对于顶点的数量，则可以不同。GraphChi执行的时候，是以internval为单位执行的。对与一个interval顶点的出边，它们会位于其它的shards结构的连续的块内。这里就体现了根据它们的源顶点来排序的意义了。

graphchi-interval

并行更新，如上面的伪代码所示，内存在的更新操作是并行进行的。这里的更新的函数一般为用户定义。由于是并行进行的，就要处理一些情况下可能出现的并发的问题,

... we enforce external determinism, which guarantees that each execution of PSW produces exactly the same result. This guarantee is straight-forward to implement: vertices that have edges with both end-points in the same interval are flagged as critical, and are updated in sequential order. Non-critical vertices do not share edges with other vertices in the interval, and can be updated safely in parallel. 

将更新之后的数据写入磁盘，将更新完整之后，需要将更新之后的数据写入磁盘，对于非这个interval的shards，只需要写入更新的一部分即可。这样每个interval的一次操作需要P(分区的数量)的非顺序写入操作

graphchi-illustration

Evolving Graphs

这里主要讲的是GraphChi如何支持修改图的结构。主要就是如何添加和删除图的边的操作。这里的主要的问题在与Shard里面的边是排好序的。这里为了解决这个问题，Shard里面的边不要求是严格有序的，它讲Shard分为P个部分，每个部分分配一个内存中的edge-buffer(p, j)结构。向里面添加边的时候，当超过一定数量的时候，就会分裂为2个新的部分。对于删除边的操作，是在运行的时候标记为删除，在写入到磁盘的时候去真正的删除。

IO复杂度

设传输的块大小为B，边的数量为|E|，IO的复杂度与这两个的除直接相关。另外最坏的情况下，还有P^2次的非顺序的磁盘操作，这样就有： \(\\ \frac{2|E|}{B} \leq Q_{B}E \leq \frac{4|E|}{B} + \Theta(P^2)\)

设计与实现 and 编程模型

GraphChi有多个来源的实现。Paper中在实现的时候的主要的优化的方法有：

存储数据格式优化，图结构个边的值分开保存。一般的情况下，只会有边的值的变化；
预处理，这里主要就是分区。一个优化的思路就是计算顶点的出度入度保存为一个文件，在一些情况下可以加快计算；
Sub-intervals，这里的优化主要就是为了处理不平衡的问题。一个子图的出边和入边的数量可能存在明显的差异，这里划分的方法就是继续讲前面的interval划分为Sub-intervals，并且会利用出度入度文件来划分。
选择调度，图的计算很多都是迭代的，当进行一些的步数之后，有些部分可能就不需要在计算了。这里的优化就是优化这个问题；

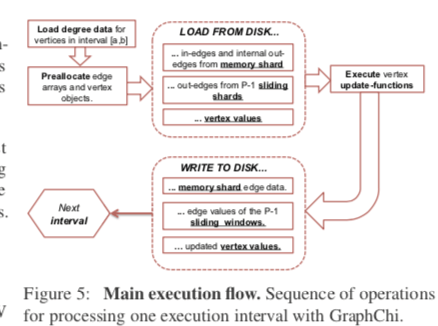
graphchi-execution

GraphChi的编程模型中边的值是可以直接修改的，但是修改顶点的值会受到内存大小的限制，所以一般的情况下是通过广播的方式。一个基本的PageRank算法的伪代码：

typedef: VertexType float
Update(vertex) begin
  var sum ← 0
  for e in vertex.inEdges() do
    sum += e.weight * neighborRank(e)
  end
  vertex.setValue(0.15 + 0.85 * sum)
  broadcast(vertex)
end

在图可以直接加载到内存的时候，可以使用直接读取修改的方法，如下面两段伪代码的对比：

typedef: EdgeType { float weight, neighbor rank; } 
neighborRank(edge) begin
  return edge.weight * edge.neighbor rank
end

broadcast(vertex) begin
  for e in vertex.outEdges() do
    e.neighbor rank = vertex.getValue()
  end 
end

typedef: EdgeType { float weight; } 
float[] in mem vert 
neighborRank(edge) begin
  return edge.weight * in mem vert[edge.vertex id]
end
broadcast(vertex) /* No-op */

评估

具体的信息可以参看[1]

参考

GraphChi: Large-Scale Graph Computation on Just a PC, OSDI’12.