The Adaptive Radix Tree: ARTful Indexing for Main-Memory Databases
### 引言
Adaptive Radix Tree是最近出现的为Main-Memory Database设计的的支持范围数据结构里面个人认为最优美的一种了,不如Masstree,Bwtree那么复杂,另外,相比于传统的一些结构如T-tree,也更好的适应了现代的多核处理器。这篇时关于Adaptive Radix Tree(ART)的基本结构的,另外有一篇时关于ART的Concurrency Control的,之后会加上。ART的主要思路时使用不同大小的Node,来减少内存使用。同时加上一些额外的如高度上的优化。
基本结构
前面提到,ART的内部Node有不同的大小。一般而言,离root比较远的Node里面保护的数据项时比较小的。一般的Radix Tree使用完整的Node的话,会浪费很多的内存,而ART就解决了这个问题:
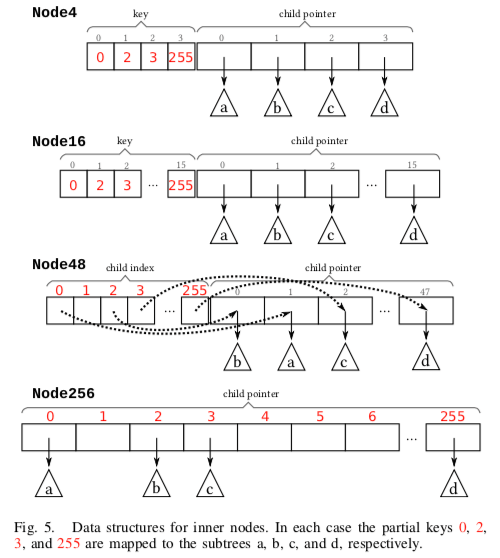
ART可以做到 With 32 bit keys, for example, a radix tree using s = 1 has 32 levels, while a span of 8 results in only 4 levels.内部 Node描述:
* Node4: The smallest node type can store up to 4 child pointers and uses an array of length 4 for keys and another array of the same length for pointers. The keys and pointers are stored at corresponding positions and the keys are sorted.
* Node16: This node type is used for storing between 5 and 16 child pointers. Like the Node4, the keys and pointers are stored in separate arrays at corresponding positions, but both arrays have space for 16 entries. A key can be found efficiently with binary search or, on modern hardware, with parallel comparisons using SIMD instructions.
* Node48: As the number of entries in a node increases, searching the key array becomes expensive. Therefore, nodes with more than 16 pointers do not store the keys explicitly. Instead, a 256-element array is used, which can be indexed with key bytes directly. If a node has between 17 and 48 child pointers, this array stores indexes into a second array which contains up to 48 pointers. This indirection saves space in comparison to 256 pointers of 8 bytes, because the indexes only require 6 bits (we use 1 byte for simplicity).
* Node256: The largest node type is simply an array of 256 pointers and is used for storing between 49 and 256 entries. With this representation, the next node can be found very efficiently using a single lookup of the key byte in that array. No additional indirection is necessary. If most entries are not null, this representation is also very space efficient because only pointers need to be stored.
对于Leaf Node,也有不同的策略:
• Single-value leaves: The values are stored using an additional leaf node type which stores one value.
• Multi-value leaves: The values are stored in one of four different leaf node types, which mirror the structure of inner nodes, but contain values instead of pointers.
• Combined pointer/value slots: If values fit into pointers, no separate node types are necessary. Instead, each pointer storage location in an inner node can either store a pointer or a value. Values and pointers can be distinguished using one additional bit per pointer or with pointer tagging.
对于inner Node,不仅仅可以表示一个串的一个字符,还可以是一个prefix,这样可以在一些情况下减少树的高度,节约内存,也可以提高缓存友好性。综合这些之后,基本的搜索算法如下:
search (node, key, depth)
if node==NULL
return NULL
if isLeaf(node)
if leafMatches(node, key, depth)
return node
return NULL
if checkPrefix(node,key,depth)!=node.prefixLen
return NULL
depth=depth+node.prefixLen
next=findChild(node, key[depth])
return search(next, key, depth+1)
此外的较为复杂的就是insert的算法了,基本的算法如下:

主要要考虑一下情况:
- 为空,则要添加节点;
- 添加到的节点时leaf节点,则要考虑到prefix;而且会对原来的leaf node做相应的修改;
- inner node对应的prefix不同时,则表明要重新处理这个prefix
- 之后查找对于对应的下一个节点,存在,递归查找,不存在,这个节点满了的话,需要拓展节点,之后添加新的子节点。
删除操作就看作是insert的逆操作即可。
分析
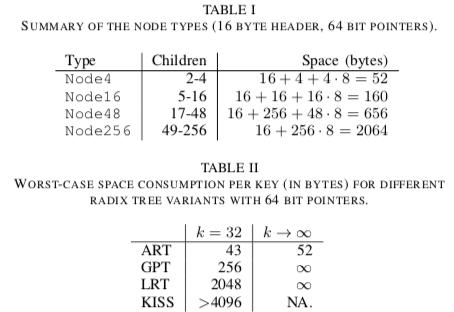
- 内存,ART一个主要优点就是更小的内存使用:
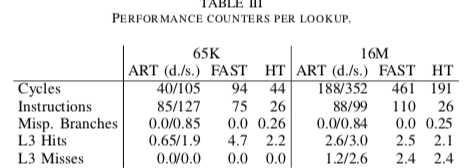
- 性能,关于性能这里只关注了缓存相关的,一个paper中的表格如下:在密集的key的情况下,ART的缓存命中率高了不少。这是因为ART的节点很”紧凑”。
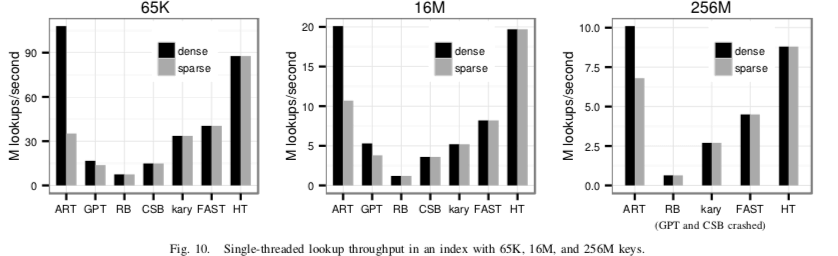
总之,ART时非常优美的,相比于其它的一些数据结构来说(Bwtree的算法复杂程度比ART高了几个数量级),简单性能有很不错。
评估
这里具体的信息可以参看[1],
参考
- The Adaptive Radix Tree: ARTful Indexing for Main-Memory Databases, ICDE 2013.
