MOSAIC -- Processing a Trillion-Edge Graph on a Single Machine

MOSAIC: Processing a Trillion-Edge Graph on a Single Machine

引言

MOSAIC是一个单机的Out-of-Core的图计算系统，能够在单机上面处理超过1万亿条边。MOSAIC的主要思路就是利用现在的一些硬件来实现更高的性能，比如NVMe的SSD和利用Interl的Xeon Phi协处理器，

 MOSAIC consistently outperforms other state-of-the-art out-of-core engines by 3.2–58.6× and shows comparable performance to distributed graph engines. Furthermore, MOSAIC can complete one iteration of the Pagerank algorithm on a trillion-edge graph in 21 minutes, outperforming a distributed disk-based engine by 9.2×.

基本架构

tiles

Out-of-Core的图计算系统首先要做的一个就是将图进行分区。MOSAIC中，图被拆分为tiles，是整个图的一个子图，不同的tiles里面不存在相同的边。关于tile的几点，

每一个tile的顶点的数量限制位Imax的值。这样的每一个顶点的在一个tile只需要一个较小的ID值就可以，比如Imax位2^16的话，只需要一个ushort就可以了。加上这个tile的全局的一个ID，使用2层的定位确定一个顶点。这个可以每一个顶点使用一个8bytes的ID要节省不少的空间。这样尺寸的另外一个好处就是可以放进缓存内。一个tiles中顶点的数量是固定的，但是边的数量不确定。
tiles之间是 Hilbert(希尔伯特)顺序，它们可以以 Hilbert顺序枚举，可以获得更加好的局部性。希尔伯特曲线在方便计算点之间的距离、找临近点的时候是一个很好的方法。MOSAIC这里用于处理图的分块。MOSAIC会在协处理器中并行地处理这些tile，MOSAIC使用的协处理器就是Xeon Phi。另外希尔伯特顺序的方式对iO的预取也很有好处，
```
While processing a tile, we can prefetch neighboring tiles from NVMe devices to memory by following the Hilbert-order in the background, which allows coprocessors to immediately start the tile processing as soon as the next vertex state array arrives.
```

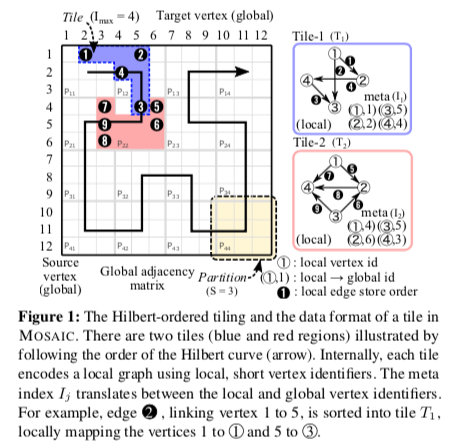
mosaic-tiles

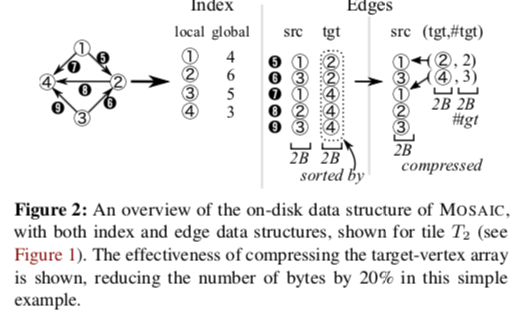
一个tile内排序好的局部的索引将局部的顶点ID映射到全局的顶点ID。边会根据目的顶点排序，这个排序的做法和GraphChi类似[2]。边根据情况保存为edge list 或者是compressed sparse rows (CSR)格式。
MASAIC中在两个层面来体现局部性：1. 在一个tile里面顺序访问边；2. 写入的局部性体现在根据来目的顶点来排序上。这个排序优化方法很常见。

mosaic-on-disk

组件

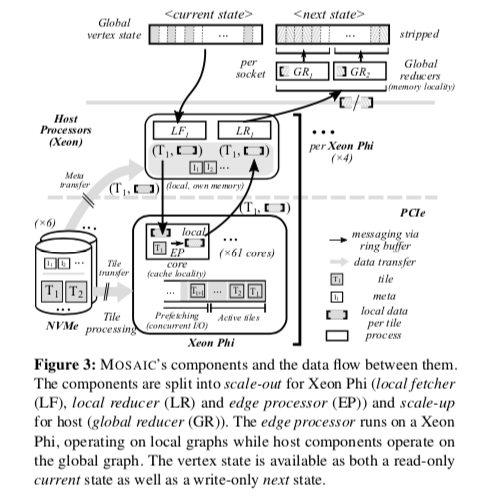
MOSAIC的主要组件及其功能，

Local fetcher (LF)，用于加速图处理中的数据流，使用预取的元数据从主机上取回顶点的状态信息，然后交给协处理器上面的edge processor处理。
Edge processor (EP)，边处理器(edge processor)在边上应用一个函数，这个函数一般就是用户使用的图算法相关的。每一个edge processor运行在协处理器的一个核心上面，处理独立的一个tiles的集合。edge processor得利用LF取回一些信息。利用顶点的状态和处理的tile里面的边的信息来应用图算法。
Local reducer (LR)，在EP完成一个本地的处理之后，LF汇集这些处理的结果，将这些结构发送给GR，用于下一次迭代的时候更新顶点的状态信息。这里会对NUMA做一些优化。
Global reducer (GR)，一个GR分配全局的顶点的一部分，从LR中获取输入然后更新顶点的状态信息。
Striped partitioning，为了更好地利用NUMA体系中的并行性，MOSAIC使用条带式的分区方式，而不是就是就是将一个连续的区域分配给一个NUMA域。

mosaic-components

执行模型

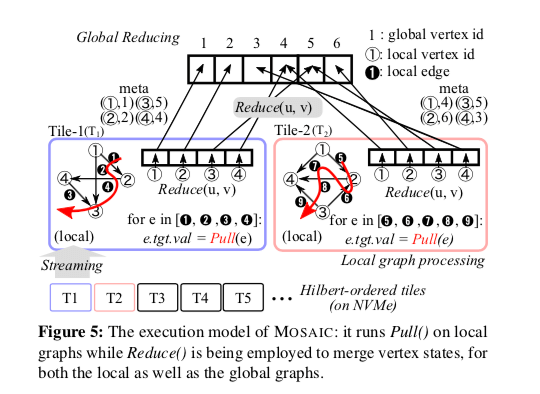
MOASIC使用常见的“think-like-a-vertex”即以顶点位中心的编程的方式。为了更好的利用多核进行了一些改进。在编程的抽象上，为了更好地利用异构计算，MOAC在Gather-Apply-Scatter的基础上拓展位Pull-Reduce-Apply (PRA)的方式。一个reduce的操作用来方便异构计算处理。一般使用这样的方式来编写图算法，

Pull(e)，使用一个图算法指定的函数在一条边计算出结果，

For Pagerank, we first pull the impact of a source vertex (the state value divided by its out-degree) and then gather this result for the state of the target vertex
by adding to the previous state.

Reduce(v1, v2)，合并处理两个来自同一个顶点的计算结果，然后给出一个合并之后的输出。这里有EP在协处理器上处理，另外也由GR在主机上面处理，
```
 For Pagerank, the reduce function simply adds both values, aggregating the impact on both vertices.
```

Apply(v)，在一次迭代的最后一步处理。用于在reduce操作完成之后处理顶点的状态，

 For Pagerank, this step normalizes (a factor α) the vertex state (the sum of all impacts on incoming vertices).

MOSAIC中，以边为中心的操作(Pull)在协处理器上进行，而以顶点位中心的操作(Apply)在主处理器上进行，而汇总结果的操作在两者上都有。

mosaic-execution

评估

这里的具体的信息可以参看[1].

参考

MOSAIC: Processing a Trillion-Edge Graph on a Single Machine, EuroSys’17.
GraphChi: Large-Scale Graph Computation on Just a PC, OSDI’12.