TinyLFU: A Highly Efficient Cache Admission Policy
0x00 引言
在工作的时候使用了caffeine这个java 本地缓存库,这个库的设计非常赞,代码也非常棒(虽然目前为止只是粗略的看了一下,如果要推荐java的开源项目看看代码,这个绝对值得推荐)。这里只关注它里面的Cache Admission Policy – TinyLFU。
0x01 基本思路
先来一张图:
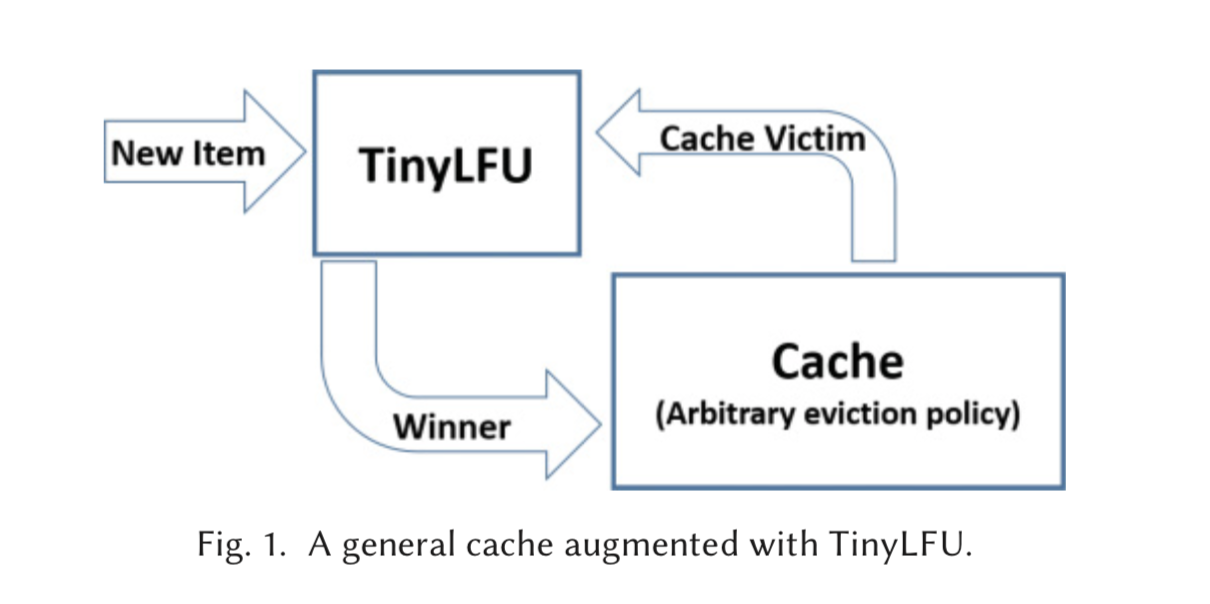
虽然论文长达31页,但是我们这里只关注其中的两个部分:
Let us emphasize that we face two main challenges. The first is to maintain a freshness mechanism in order to keep the history recent and remove old events. The second is the memory consumption overhead that should significantly be improved upon in order to be considered a practical cache management technique.
- 如何保存访问信息;
- 如何减少内存使用;
0x02 保存访问信息
我们知道LFU中间的F代表的是Frequency。但是保存每一个数据项的访问频率信息是不现实的,这样会带来巨大的开支。Tiny-LFU使用的是CM-Sketch,作为一个近似计算访问次数据结构。值得注意的是CM-Sketch记录的是访问次数,而不是频率,而且从访问次数中是代表不了频率信息的。这里就是Tiny-LFU一个创新的地方了:
Every time we add an item to the approximation sketch, we increment a global counter S. Once the value of this counter S reaches the sample size (W), we divide S and all other coun- ters in the approximation sketch by two. Notice that immediately after the reset, S = W /2.
This division has two interesting merits. First, it does not require much extra space as its only added memory cost is a single counter of Loд(W ) bits. Second, this method increases the accuracy of high-frequency items as we show both analytically and experimentally.
巧妙的在合适的条件下将原有的统计信息减半,将这些信息代表频率信息。显然在这个算法中,我们并不关心频率具体是多少,在意的是访问频率谁高谁低,这个方法就能很好的解决这个问题。这也是这个算法最惊艳的地方。
0x03 减少内存使用
这里主要来自两个方面:
First, we reduce the size of each of the counters in the approximation sketch. Second, we reduce the total number of counters allocated by the sketch.
Small Counters
正如前文所说,由于统计信息会在合适的时机减半,此外也只关注大小的信息不关心具体的数据,使用counter就可以使用很少的bit:
If a sketch holds W unique requests, it is required to allow counters to count until W (since in principle an item could be accessed W times in such a sample), resulting in Loд(W ) bits per counter, which can be prohibitively costly. Luckily, the combination of the reset operation and the following observation significantly reduces the size of the counters.
reduce the total number of counters
Doorkeeper是approximate counting scheme前面的一个bloom filter,一个元素添加的时候,如果不在这个里面,则先添加到Doorkeeper里面,如果存在,则直接添加到主结构里面。每次访问元素时,如果在Doorkeeper里面,那么就是主结构里面的数值加上1,如果不存在就只使用主结构里面的数据。这么做的原因是可以减少主结构的大小。每一次reset操作会清空Doorkeeper。
0x04 W-TinyLFU
W-TinyLFU近似在Tiny-LFU前面添加了小的LRU,大约只占1%的数据。用来解决突发的稀疏流量:
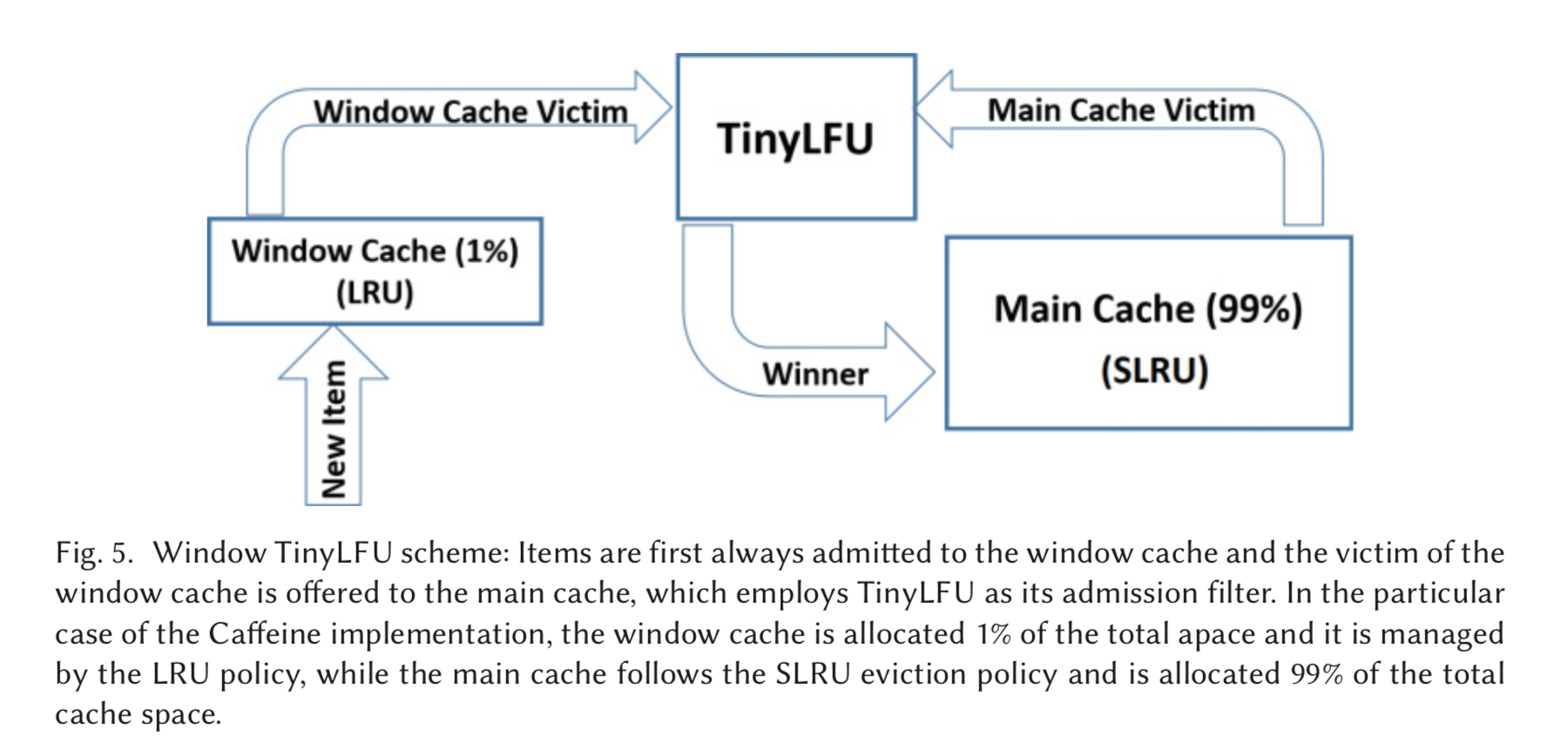
一般基于频率的cache management policy 都存在这个问题:一个突发的频繁访问少量的对象,大部分的范围都集中,这样就会是其它的数据项的频率估计出现较大的误差。这里使用的方法就是在前面加一个小的LRU,挡住这些频繁被访问的项来解决这个问题。 对于main cache ,使用之前存在的算法, 这里存在的是SLRU,具体参考SLRU的文章:
we employ the SLRU eviction policy (Karedla et al. 1994). The A1 and A2 regions of the SLRU policy in the main cache are divided such that 80% of the space is allocated to hot items (A2) and the victim is picked from the 20% nonhot items (A1), as recommended by (Karedla et al. 1994).
这样也就是说,Tiny-LFU主要的工作还是在以小的空间,时间成本来估算访问频率,同时解决突发访问的问题。此外一个好玩的地方就是:
The Caffeine simulator implements the following schemes: Belady’s optimal (Belady 1966), an unbounded cache, LRU, MRU, LFU, MFU, FIFO, Random, TinyLFU, W-TinyLFU, Clock (Corbato 1968), S4LRU (Huang et al. 2013), SLRU (Karedla et al. 1994), MultiQueue (Zhou et al. 2001), Sampled LRU (Psounis and Prabhakar 2002), Sampled MRU (Psounis and Prabhakar 2002), Sampled LFU (Psounis and Prabhakar 2002), Sampled MFU (Psounis and Prabhakar 2002), Sampled FIFO (Psounis and Prabhakar 2002), 2Q (Johnson and Shasha 1994), TuQueue (OpenBSD 2014), LIRS (Jiang and Zhang 2002), Clock-Pro (Jiang et al. 2005), ARC (Megiddo and Modha 2003, 2006), CAR (Bansal and Modha 2004), and CART (Bansal and Modha 2004).
可以说是很全了。2333333.
参考
- Gil Einziger, Roy Friedman, and Ben Manes. 2017. TinyLFU: A Highly Efficient Cache Admission Policy. ACM Trans. Storage 13, 4, Article 35 (November 2017), 31 pages. https://doi.org/10.1145/3149371 .
