Cuckoo Filter: Practically Better Than Bloom
0x00 引言
Cuckoo Filter是一种功能类似Bloom Filter的数据结构,它最大的一个特点就是支持删除,前在很多的情况下都实现了比Bloom Filter更加好的性能,
the cuckoo filter, a practical data structure that provides four major advantages.
1. It supports adding and removing items dynamically;
2. It provides higher lookup performance than traditional Bloom filters, even when close to full (e.g., 95% space utilized);
3. It is easier to implement than alternatives such as the quotient filter; and
4. It uses less space than Bloom filters in many practical applications, if the target false positive rate ε is less than 3%.
0x02 基本思路
这个类似的思路在SOSP‘11上面的一篇文章就出现了[2]。这里在一般的的cuckoo hash table上面的一些修改就是:只存储fingerprints就可以了,为了支持cuckoo hash多个hash函数的操作,这里使用了partial-key cuckoo hashing的方法。
Insert操作
这里直接算法的伪代码进行说明,
Algorithm 1: Insert(x)
f = fingerprint(x);
i1 = hash(x);
i2 = i1 ⊕ hash(f);
if bucket[i1] or bucket[i2] has an empty entry then
add f to that bucket;
return Done;
// must relocate existing items;
i = randomly pick i1 or i2;
for n = 0; n < MaxNumKicks; n++ do
randomly select an entry e from bucket[i];
swap f and the fingerprint stored in entry e;
i = i ⊕ hash( f );
if bucket[i] has an empty entry then
add f to bucket[i];
return Done;
// Hashtable is considered full;
return Failure;
这里的一个hash值就是直接以一个hash函数计算的,另外一个hash值则是fingerprint和第一个hash值的xor。这里和SILT[1]中在slot中保存另外一个hash值的方法有些区别。
Loopup操作
Loopup操作则简单很多,
Algorithm 2: Lookup(x)
f = fingerprint(x);
i1 = hash(x);
i2 = i1 ⊕ hash(f);
if bucket[i1] or bucket[i2] has f then
remove a copy of f from this bucket;
return True;
return False;
Delete操作
这里删除的操作也非常简单,
Algorithm 3: Delete(x)
f = fingerprint(x);
i1 = hash(x);
i2 = i1 ⊕ hash(f);
if bucket[i1] or bucket[i2] has f then
remove a copy of f from this bucket;
return True;
return False;
Paper中虽然说了一堆的好话,这里还是有一些缺陷的,不过暂时好像没有好的解决办法。注意这里是可以一个buckets里面是可以存在重复的footprint的,如果不要求删除,则可以让其不出现重复的。
Note that, to delete an item x safely, it must have been previously inserted. Otherwise, deleting a non-inserted item might unintentionally remove a real, different item that happens to share the same fingerprint. This requirement also holds true for all other deletion-supporting filters.
这里在实际的应用中的解决办法就是在Cuckoo Filter返回可能存在时,在去实际保存数据的结构里面查找(比如在LSM-tree里面就是保存在SSTeabls里面),在确认存在之后才去删除操作,这样就可以做到安全删除了。
0x03 一些证明
算法是很简单容易理解的,这里主要是要证明一些东西。下面是会使用到的一些符号:
ε target false positive rate f fingerprint length in bits
α load factor(0≤α≤1)
b number of entries per bucket
m number of buckets
n number of items
C average bits per item
f bits number of footprint
Minimum Fingerprint Size
emmmm,这里Paper中先是通过一个证明来证明了,
We conclude that 4^bf must be Ω(n) to avoid a non-trivial probability of failure, as otherwise this expectation is Ω(1). Therefore, the fingerprint size must be f = Ω(log n/b) bits.
This result seems somewhat unfortunate, as the number of bits required for the fingerprint is Ω(log n); recall that Bloom filters use a constant (approximately ln(1/ε) bits) per item. We might therefore have concerns about the scalability of this approach.
f = Ω(log n/b),看上去不是很好。但是然后又说在实际中可以实现很好的效果,
For a Bloom filter, achieving ε = 1% requires roughly 10 bits per item, regardless of whether one thousand, one million, or billion items are stored.
...
We find that, for practical purposes, it can be treated as a reasonable-sized constant for implementation. Figure 2 shows that for cuckoo filters targeting a few billion items, 6-bit fingerprints are sufficient to ensure very high utilization of the hash table.
说明在实际应用中内存的效率可以很高。
Optimal Bucket Size
内存的消耗主要就是下面的式子: \(C = \frac{table\;size }{\#\;of\;items} = \frac{f\cdot(\#\;of\;entries)}{\alpha\cdot(\#\;of\;entries)} = \frac{f}{\alpha}\quad bits.\)
-
更大的buckets会提高表的利用率,即更高的α,
With k = 2 hash functions, the load factor α is 50% when the bucket size b = 1 (i.e., the hash table is directly mapped), but increases to 84%, 95% or 98% respectively using bucket size b = 2, 4 or 8. -
更大的buckets要求更大的f来保持相同的false positive rate。这里是一个证明:
这里可以看出来f和α都和buckets的大小密切相关。有根据上面的等式,有: \(C\leq \lceil\log_{2}(1/\epsilon)+log_{2}(2b)\rceil\;/\;\alpha, \quad Eq. (7)\)
where α increases with b. For example, when b = 4 so 1/α ≈ 1.05, Eq. (7) shows cuckoo filters are asymptotically better (by a constant factor) than Bloom filters, which require 1.44 log2 (1/ε) bits or more for each item.
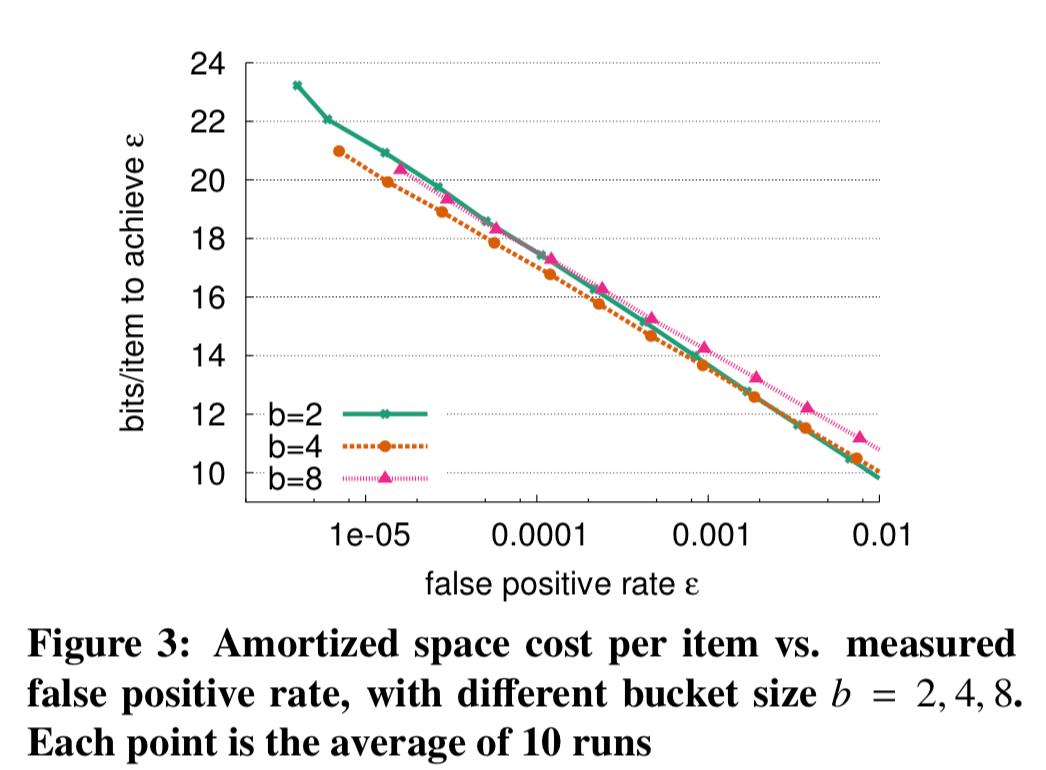
这里的结论:
the space-optimal bucket size depends on the target false positive rate ε: when ε > 0.002, having two entries per bucket yields slightly better results than using four entries per bucket; when ε decreases to 0.00001 < ε ≤ 0.002, four entries per bucket minimizes space.
In summary, we choose (2, 4)-cuckoo filter (i.e., each item has two candidate buckets and each bucket has up to four fingerprints) as the default configuration,...
这里就是使用了2个hash值和每个buckets 4项的配置。
Semi-sorting Buckets to Save Space
这里使用了一种叫做semi-sorting buckets的优化方法。这里使用的方式就是将一个bucket里面的数据排序,因为footprint的顺序对正确性没有影响。因为f = 4 bits and b = 4为例,排序之后值的可能取值只有3876个,这样就可以预先计算出可能的取值,保存在一个数组里面,然后在table里面保存的这个值在数组中的index,就只要12bits,一个bucket就节省了4bits。这里3876计算的方法也显然,不过算起来可能比较麻烦。不过对于学CS的人来说,一个脚本就可以了:
s = set()
for i in range(0, 16):
for j in range(i, 16):
for k in range(j, 16):
for u in range(k, 16):
l = [i, j, k, u]
l.sort()
s.add(l[0]+(l[1]*16 if l[1] != l[0] else 0) + (l[2]*16*16 if l[2] != l[1] else 0)\
+ (l[3]*16*16*16 if l[3] != l[2] else 0))
print(len(s))
0x04 评估
具体的信息参考[1]

参考
- Cuckoo Filter: Practically Better Than Bloom, CoNEXT’14.
- SILT: A Memory-Efficient, High-Performance Key-Value Store, SOSP’11.
- Scalable, High Performance Ethernet Forwarding with CUCKOOSWITCH, CoNEXT ‘13.
