Tree Indexing on Solid State Drives
0x00 引言
这篇文章讨论的是如何在SSD上面优化树形索引。这个设计主要基于下面的几个在SSD上面设计indexing的原则:
- 将随机写转化为顺序写,这个在SSD和HHD上面都是一样的思路;
- 将随机写限制在一个小的区域内,SSD在一个小的区域内(512KB-8MB)的随机写的性能能够比得上顺序写;
- 支持多个page的IO操作。
... shows that the FD-tree captures the best of both search and insertion performance among all competitors. In particular, it is 5.7-27.9X, 1.4- 1.6X and 3.7-5.5X faster than B+-tree, LSM-tree and BFTL, respectively, under various mixed workloads on an Mtron SSD, and it is 1.7-3.6X, 1.4-1.8X, and 1.9-3.4X faster than B+-tree, LSM-tree and BFTL, respectively, on an Intel SSD.
0x01 基本思路
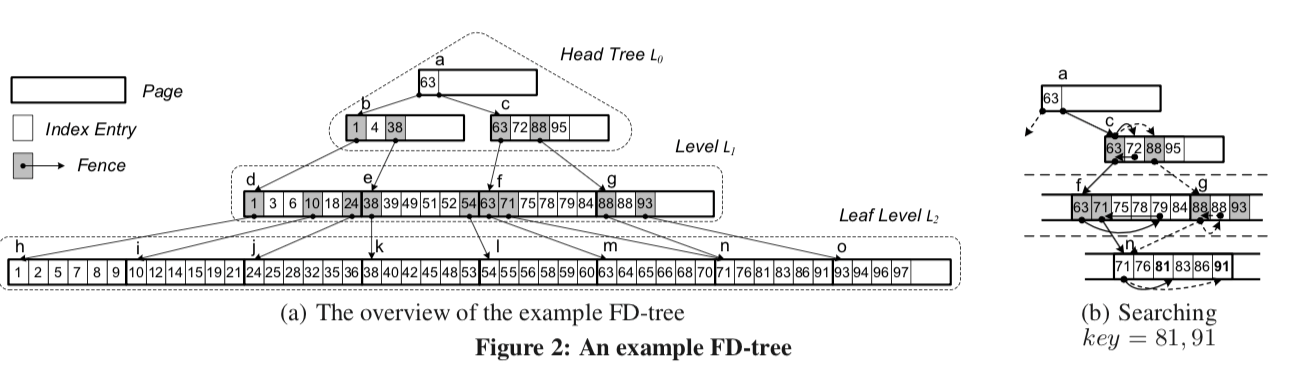
| 如上面的图所示,FD-tree的设计可以说是结合Btree和LSMtree的特点。FDtree有若干层组成。在FDtree的上层一个HeadTree。这个HeadTree实际上就是一棵小的Btree。每一个结点的大小为page的大小(记为B)。其它的处于HeadTreex下面的层,都是一个排序好的联系的pages组成的。每一个HeadTree的非叶子结点都包含指向L1层的指针。其余的层也保护指向下一层的指针,这里的指针不像Btree。 每一层都一层的容量,即保护entries的个数,记为 | Li | 。相邻层数之间的数量是一个倍数的关系,即 | Li+1 | = k · | Li | (0 ≤ i ≤ l − 2), | Li | = ki · | L0 | 。HeadTree即为L0,更新操作都是现在这里执行,它的大小达到一定的阈值的时候,会被合并到下面的level中,这里的思路和LSM-tree很相似。根据前面的设计原则,HeadTree的大小被称为 locality area, 通常情况下为128KB – 8MB。在FDtree中的level中的entries分为两种类型: |
-
Index Entry, 包含了三个字段:key;record id(rid),这个rid是为了找到对应的value;另外就是type字段知名entry的类型。type=filter的时候就代表这个记录已经被删除了,type=normal的时候代表这个就是一个平常的记录。
-
Fence , 包含了三个字段: key;type,同样表示类型;pid字段就是它指向的下一层的一个page。这里实际上就相当于一个指针。这里满足下面两个条件,
INVARIANT 1. The first entry of each page is a fence. INVARIANT 2. The key range between a fence and its next fence at the same level is contained in the key range of the page pointed by the fence.type的取值取决于这个fence带的key是来自它这一层还是下一层,将fence分为两种:type=External代表了它带的key来自下一层,type=Interbal就代表key就来自这一层,这么做的原因是当这一页的第一项不是external fence的时候,为了满足前面的INVARIANT 1,就添加这样一个分册。它指向下一层包含对应key的page。如上面图中的倒数第二层的88,每一个page最多只会包含一个internal fence。这么做的原因可以从图中看出来。标记为g的page对于的88的key它不好从下一层选择key,这样就直接冲本层选择一个。由于internal fence的存在是为了满足INVARIANT 1,所以最对就只要一个就可以了,多的也没有存在的意义。
... the number of external fences in Li is the number of pages in Li+1 , i.e. |Li+1 |/f , where f is the number of entries in a page. The number of internal fences in Li is at most |Li|/f, because each page contains at most one internal fence. The maximum total number of fences in Li, (|Li | + |Li+1 |)/f , should be smaller than the number of entries in Li, obtaining k < f − 1.
这里这样的设计于fraction cascading很相似。
0x02 操作
这重要的还是如何在这样的设计上面实现应有的操作:
-
查找。要区分范围查找和点查找这里的思路也和LSM-tree的方法类型,都是从上到下一层层查找,对于key可能存在于的page,使用二分查找即可。查找的目标是等于key或者是小于这个key的最大值。对于点查找,如果查找到等于的,则可以发挥信息。如果是范围查找,则还得深入下面的level中查找。这里还要处理filter类型的entry和normal类型的entry。
The range search is similar to that for the point search except that it may fetch multiple pages in each level. Given the fences satisfying the predicate in the current level Li, we are aware of the number of pages that will be scanned in the next level Li+1 before fetching those pages. Moreover, those pages are stored contiguously. These properties provide an opportunity to fetch the exact number of matched pages in the next level in a I/O operation by using multi-page I/O optimization (P3). -
添加,先添加到L0,L0达到一定的大小之后合并到L1.
-
合并,这里看起来就像LSM-tree的套路。这里就是一个两个已经排好序的数组的合并的过程。合并的时候合并到的一层的external fence必须都要保留,而internal fence根据实际情况选择。由于这里合并之后存在的page改变了,这样也就要求上面的层的external fence的数据也必须同步更新:
At the same time, the new levels Lj(0 ≤ j < i) are rebuilt with the external fences constructed from the newly generated Li. That is, given two adjacent levels, Li−1 and Li, the merge process generates i + 1 new sorted runs to update all levels from L0 to Li. If the new Li exceeds its capacity, Li and Li+1 are merged.可以看出来,这样导致的级联的更新是这个FDtree一个很大的缺点。
-
删除,这个的逻辑也和LSM-tree的差不多。
The first step is to perform the deletion on the head tree L0, be- cause random writes on the head tree are limited within a locality area, and are very efficient. Next, we perform deletion in the other levels by inserting a special entry called a filter entry .... During the merge, physical deletions are performed in batches. When a filter entry encounters its corresponding phantom entry, both entries are discarded, and will not appear in the merge result. Thus, a deletion is physically completed. -
更新,就相当于删除原来的数据在添加新的数据。
0x03 成本分析和成本模型
关于复杂度等的分析可以参考[1].

0x04 评估
这条咸鱼认为FD-tree看起来没有特别的长处,还有不少的缺点。具体的评估数据可以参考[1].
LSbM-tree: Re-enabling Buffer Caching in Data Management for Mixed Reads and Writes
0x00 引言
这篇Paper主要讨论的是Log-Structured buffered-Merge tree的设计。要解决的问题是在LSM-tree的频繁的合并操作时,会使得buffer cache里面的数据失效,需要重新load数据,这个导致性能的降低。LSbM-tree基本思路是使用一个在磁盘上面保存的buffer (on-disk compactionbuffer)来处理一些具有局部特性的读和写操作。
We have implemented LSbM based on LevelDB. We show that with a standard buffer cache and a hard disk, LSbM can achieve 2x performance improvement over LevelDB. We have also compared LSbM with other existing solutions to show its strong effectiveness.
0x01 基本思路
下面是LSbM-tree的一个基本的结构图。从图中可以看出来这里的compaction buffer是在每一次层是一个list。
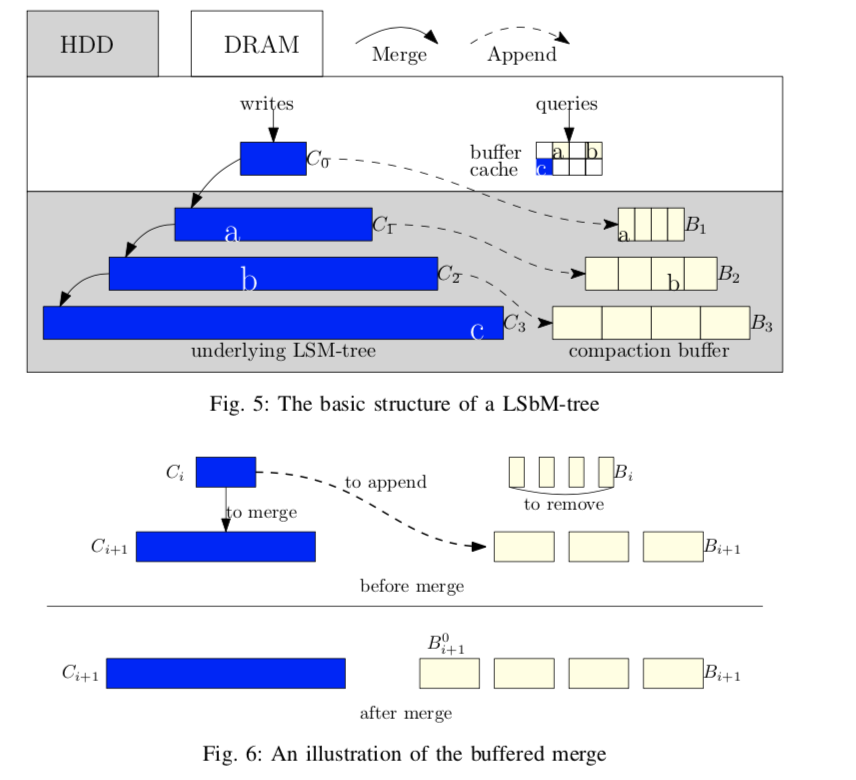
这里的compaction buffer期望保存的数据是频繁访问的数据。使用这里的第一个问题就是如何找出这些数据。这里使用了一个buffered merge的算法:首先,当一层的数据merge到下面的一层的时候,与此同时,这写数据会被当作下面一层的compaction buffer中的第一个。这里是直接利用的原来上面一层的数据,使用不会导致额外的IO操作。这个时候就可以将上面一层的compaction budder删除了,因为已经没什么用了。当合并的时候,如果发现了重复的key,就可能这一层的数据保护了重复的key,也就意味着这里的buffer可能有的数据已经过时了。LSbM-tree会将这一层的compaction buffer冻结,知道这一层合并到下一层之后重新启用,
If the size of Ci+1 is smaller than the data compacted into it, there must exist repeated data. When repeated data are detected, LSbM freezes Bi+1. When Ci+1 becomes full and is merged down to next level, Bi+1 is unfrozen and continues serving as the compaction buffer list of Ci+1.
合并的时候会删除Bi。突然的删除可能导致突然性的性能降低和延时增加。未来解决这个问题,这里采用了类似bLSM-tree的方法。在这里LSbM-tree在一层主要的数据Ci分为了两个部分Ci和Ci’。当Ci中被添加了多少数据,Ci‘中就会有多少数据被合并到下面一层,这两个数据的和是相等的的。这样,到Ci满了的时候,Ci‘就会是空的。之后就像回到了之前。基本的算法如下:

Buffer毕竟是冗余的数据,不会被一直保留。当一层里面的buffer的一个文件的被cache的数据小于一定的阈值的时候,这个文件就会删除:

0x02 算法上面的改变
在添加了Compaction Buffer之后,LSM-tree的其它的一些方法如查找的操作也要有相应的变化。对于点查询来说,添加的就是在一层查找的时候要先看一下Compaction Buffer里面的有木有:

对于范围查询,也是差不多的改动,这里要注意的是Compaction Buffer的数据是不完整的,

0x13 评估
这里可以参考[2].
参考
- Tree Indexing on Solid State Drives, VLDB 2010.
- LSbM-tree: Re-enabling Buffer Caching in Data Management for Mixed Reads and Writes, ICDCS’17
