Monkey -- Optimal Navigable Key-Value Store

Monkey: Optimal Navigable Key-Value Store

0x00 引言

Monkey解决的一个问题就是如何寻找LSM-Tree中最佳的Bloom Filter的设置的问题。在LSM-Tree中，查找的时候会先使用Bloom Filter(or其它类似的数据结构)来过滤不必要的查询，减少在磁盘的数据上面查找的次数。在一般的基于LSM-Tree的系统上面，这个Bloom Filter的false positive rates在每一次层都是固定的，比如均为0.82%。在实际的系统，每一层的数据访问的量和访问的成本是不一样的，这里一个显然的思路就是将访问次数过多的、访问成本更加高层的Bloom Filter的false positive rates更加低，能获得更好的性能。下面的图就基本展示它的基本的原理，

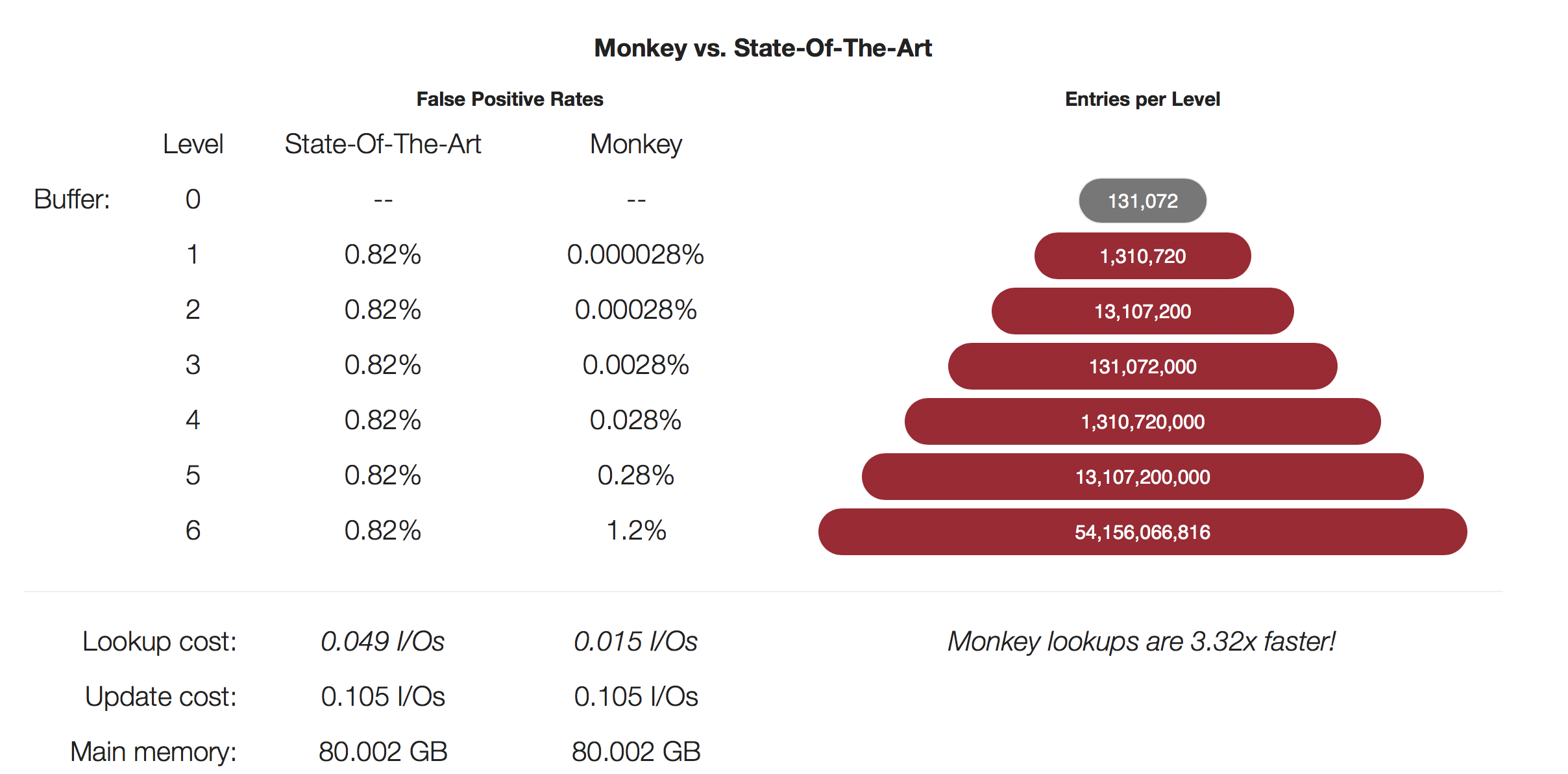
monkey-priciple

0x02 基本思路

下面是在Paper中出现的一些符号的解释：

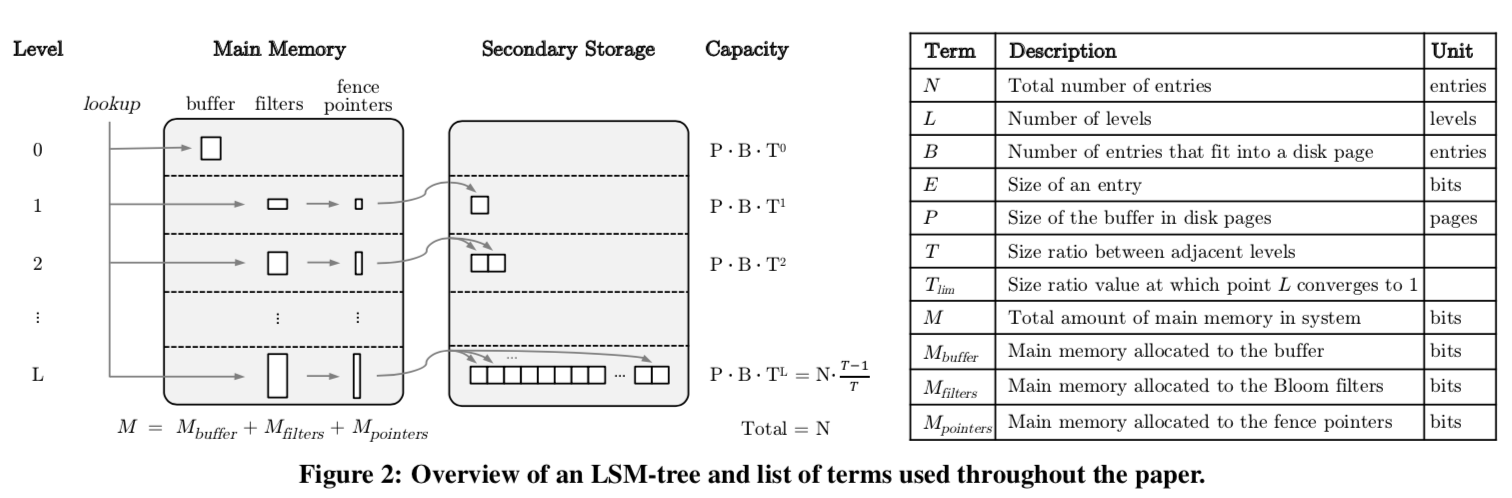
monkey-terms

关于Tiered和Leveled合并方式的区别可以参考相关资料。这里先是一些基本的知识：

LSM-Tree高度的证明

设内存中一个buffer的大小计为M_{buffer}，大小记为B，内存中buffer的数量为P，E为数据项的平均大小，这样可以得到LSM-Tree的层高为(每一个符号的意思参照上面图中的表): $\\ L = \lceil log_{T}( \frac{N \cdot E}{M_{buffer}} \times \frac{T-1}{T}) \rceil$ 证明: 假设每一层都达到最大的容量，则总的数据项有: $\\ 第i层的大小为 P \cdot B \cdot T^{i}, \\ 则总数有N = P \cdot B \cdot T^{0} + P \cdot B \cdot T^{1} + \cdot\cdot\cdot + P \cdot B \cdot T^{L}, \\ 最后一层占总数的比例 F = \frac{T^{L}}{\frac{1-T^{L+1}}{1-T}}, \\ 当L很大时，可以表示为 F = \frac{T^{L}(1-T)}{T(\frac{1}{T}-T^{L})} = \frac{T-1}{T}，这里也可以看作是一个上限, \\ 得 P \cdot B \cdot T^{L} = N \cdot \frac{T-1}{T}, 又M_{buffer} = P \cdot B \cdot E,$ 向上取整即可得， $\\ L = \lceil log_{T}( \frac{N \cdot E}{M_{buffer}} \times \frac{T-1}{T}) \rceil$

这里的T有一个值的大小限制为： $\\ T \in [2,\frac{N \cdot E}{M_{buffer}}]$

Bloom Filter的false positive rate的证明

假设hash函数生成的hash都是完全均匀的，设bits数为m，数据项数为n(这里的m一般远大于n)，hash函数的个数为k。在添加了一个元素之后，一个bit没有被设置的概率为 $\\ p_{1} = (1 - \frac{1}{m})^{k},$ 则添加了n个元素之后没有被设置的概率为 $\\ p_{n} = (1 - \frac{1}{m})^{k \cdot n}$ 那么对于一个不存在的值，如果它是false positive的情况，则有 $\\ p_{false} = [ 1 - (1 - \frac{1}{m})^{kn}]^{k}$ 根据e的定义，转化一下有 $\\ p_{false} = [ 1 - (1 - \frac{1}{m})^{kn}]^{k} = [ 1 - (1 - \frac{1}{m})^{-m \cdot \frac{-1}{m}kn}]^{k}$ 当m很大是可以看作为 $\\ p_{false} = [ 1 - (1 - \frac{1}{m})^{-m \cdot \frac{-1}{m}kn}]^{k} = (1 - e^{-kn/m})^{k}$

最优K的证明

这里就可以抽象为求下面函数在一定约束条件下的最小值, $\\ f(x) = (1 - e^{ a \cdot x})^{x}, x > 0, 其中 a = - \frac{n}{m}, m > 0, n > 0; \\ \ln(f(x)) = x \cdot \ln(1-e^{ a \cdot x}), \\ \frac{d\ln(f(x))}{dx} = \ln(1-e^{ a \cdot x}) - \frac{ax \cdot e^{ax}}{1 - e^{ax}}$ 这里就变成了一个利用导函数求极小值， $\\ 上述等式成立时有， 1-t = t, 即 t = \frac{1}{2}, 即 e^{ax} = \frac{1}{2}, 且满足取极小值的条件，\\ 即 -\frac{n}{m}x = \ln(\frac{1}{2}), 即可得 x = \frac{m}{n}\ln2.$ 即k的最优取值。另外这里m/n的最优取值很显然, $\\ \frac{m}{n} = -\frac{\ln p_{false}}{2\cdot \ln2} \approx -1.44 \cdot \log_{2} p_{false}.$

Bloom Filter的FPR和内存消耗

假设这里取最优的K的个数，则 $\\ p_{false} = (1 - e^{-\frac{m}{n}\ln2\cdot \frac{n}{m}})^{\frac{m}{n}\ln2} \to m = -\frac{n\ln p_{false}}{2\cdot \ln2}, 即 bits = -entries\cdot\frac{\ln(FPR)}{2\cdot\ln2}, \\ p_{false} = e^{-\frac{m}{n}\cdot 2\ln2}, 即 FPR = e^{-\frac{bits}{entries}\cdot 2\cdot\ln2}$ Monkey主要是在以下三个因素上面达到一个最佳的平衡，下面的表是一些成本计算的公式，下面会一一给出证明：

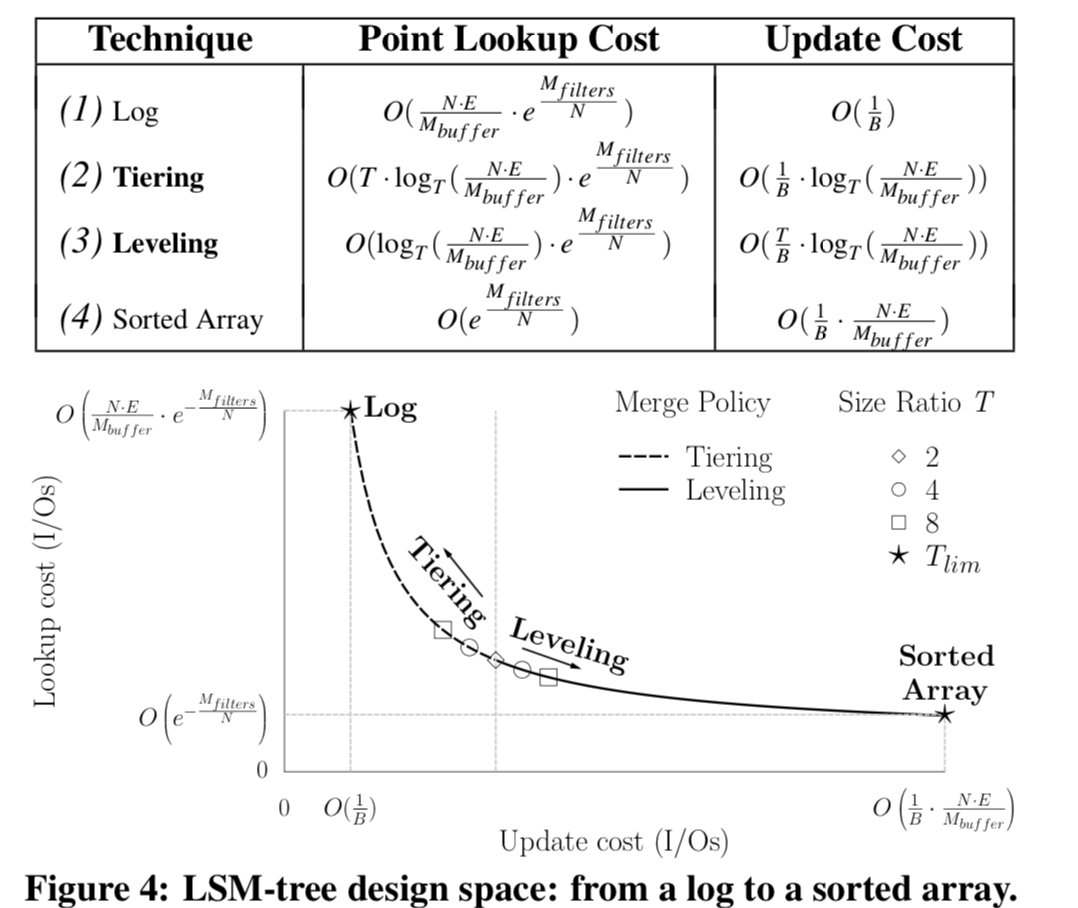
monkey-design-space

lookup cost & update cost

有前面的Bloom Filter的FPR得到，每一次查询的次数的约为, $\\ O(e^{-\frac{M_{filters}}{N}}), M_{filters}为分配给Bloom Filter的内存的量，N为数据项的量,$ 对于Tiered LSM-tree，查询复杂度为， $\\ O(L \cdot T \cdot e^{-\frac{M_{filters}}{N}}), L层，每层的数量为T,每一个的复杂度为O(e^{-\frac{M_{filters}}{N}})$ 对于更新的复杂度，为 $\\ 每次合并的每项的成本为O({\frac{1}{B}}),引起合并的次数的级别为O(L)，则可得O(\frac{L}{B}),$ 对于Leveling LSM-tree就是一个T上面的变化，点查询和更新分别为， $\\ O(L \cdot e^{-\frac{M_{filters}}{N}}), O(\frac{L \cdot T}{B})$ 由前面的得到的L， $\\ L = \lceil log_{T}( \frac{N \cdot E}{M_{buffer}} \times \frac{T-1}{T}) \rceil \to O(\log_{T}\frac{NE}{M_{buffer}}),$ 所以得到Tiering和Leveling LSM-tree的点查询的复杂度分别为(这里就可以看出来后者是为查询优化的):

$\\ O(T \cdot \log_{T}\frac{NE}{M_{buffer}} \cdot e^{-\frac{M_{filters}}{N}}), O(\log_{T}\frac{NE}{M_{buffer}} \cdot e^{-\frac{M_{filters}}{N}})$ 同理，得到点更新的复杂度为(这里就可以看出来前者是为更新优化的)， $\\ O(\frac{1}{B} \cdot \log_{T}\frac{NE}{M_{buffer}}), O(\frac{T}{B} \cdot \log_{T}\frac{NE}{M_{buffer}})$

main memory footprint

这里的内存消耗主要就考虑两个部分，一个是在内存的M_{buffer}，主要就是memtable。其余的就是Bloom Filters，Bloom Filters在下面证明，

0x02.8 Design Space

调优主要就是在以下的几个参数的调整：

the merge policy (tiering vs. leveling),
the size ratio T between levels,
the allocation of main memory among the buffer $M_{buffer}$ and the Bloom filters,
the allocation of $M_{filters}$ among each of the different Bloom filters,

在上面的参数设置中，它们之间是存在一些冲突关系的：

不同得M_{filters}之间内存分配的冲突，
M-buffer和和$M_{filters}$之间内存分配的冲突;

size ratio和merge policy的各种的取舍:

This is complicated because workloads consist of different proportions of (1) updates, (2) zero-result lookups, (3) non-zero-result lookups, and (4) range lookups of different selectivities. Decreasing the size ratio under tiering and increasing the size ratio under leveling improves lookup cost and degrades update cost, but the impact and rate of change on the costs of different operation types is different.

下面的内容依然会有很多符号以及更多的推导，

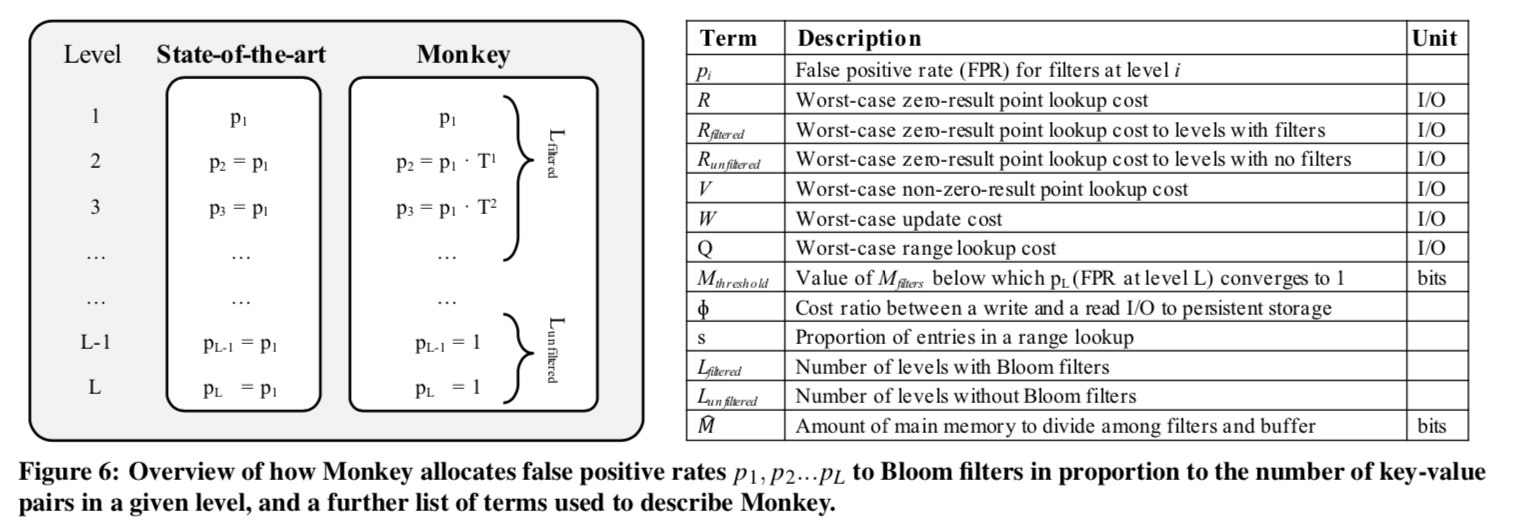
monkey-fpr

0x03 Minimizing Lookup Cost

这里使用符号R表示在查找最坏的情况下查找不存在的数据得成本，设p_{i}为每一层的Bloom Filter的FPR，则 $\\ R = \left\{ \begin{array}{ll} \sum_{i=1}^L p_{i}, & \textrm{leveling 模式} \\ (T-1) \cdot \sum_{i=1}^L p_{i}, & \textrm{tiering 模式} \end{array} \right.$ 这里就是每一层求和，在tiering模式中每一层最多为T-1个。根据前面LSM-tree高度的推导，和相邻层之间项数的倍数关系，可以得到第i层最大的项数的计算公式： $\\ 第i层的项数 n_{i} = \frac{N\cdot\frac{T-1}{T}}{T^{L-i}}, 则第i层的bits数量为m_{i} = -\frac{N}{T^{T-i}}\cdot\frac{T-1}{T}\cdot\frac{\ln(p_{i})}{2\cdot\ln2} ,\\ 则内存消耗的和 M_{filters} = -\frac{N}{2\cdot\ln2}\cdot\frac{T-1}{T}\cdot\sum_{i=1}^L\frac{\ln p_{i}}{T^{L-i}},$ 这里要实现的就是在给定$M_{filters}$的情况下，使得R最最小，这里调整的参数就是Pi，这里先给出结论 $\\ 对于Leveing模式: \\ p_{i} = \left\{ \begin{array}{ll} 1, & 当i > L_{filtered} \\ \frac{(R-L_{unfiltered})\cdot (T-1)}{T^{L_{filtered+1-i}}}, & \textrm{其它} \end{array}\right. \\ s.t. \quad 0 < R \leq L \; and \; 1 \leq i \leq L \; and \; L_{filtered} = L - max(0,\lfloor R-1\rfloor)\\ .\\ 对于Tiering模式: \\ p_{i} = \left\{ \begin{array}{ll} 1, & 当i>L_{filtered} \\ \frac{(R-L_{unfiltered})\cdot (T-1)}{T^{L_{filtered+1-i}}}, & \textrm{其它} \end{array}\right. \\ s.t. \quad 0 < R \leq L\cdot(T-1) \; and \; 1 \leq i \leq L \; and \; L_{filtered} = L - max(0,\lfloor\frac{R-1}{T-1}\rfloor) \\ 在这里\; L = L_{filtered} + L_{unfiltered},分别代表使用filter和没有使用的。$

证明

基本就在一些约束条件下的最优化的问题，使用的方法也就是常见的拉格朗日乘数法，TODO。有了上面的公式之后，这里要做的两件时间就是 1. 找到最佳的$L_{filtered}$, 2. 设置每一个level的FPR。

0x04 Predicting Lookup and Update Costs

这里讨论是在上面设计决策下，对性能的具体影响的分析，这里也是一大推的公式，一下面是一个总结的表，

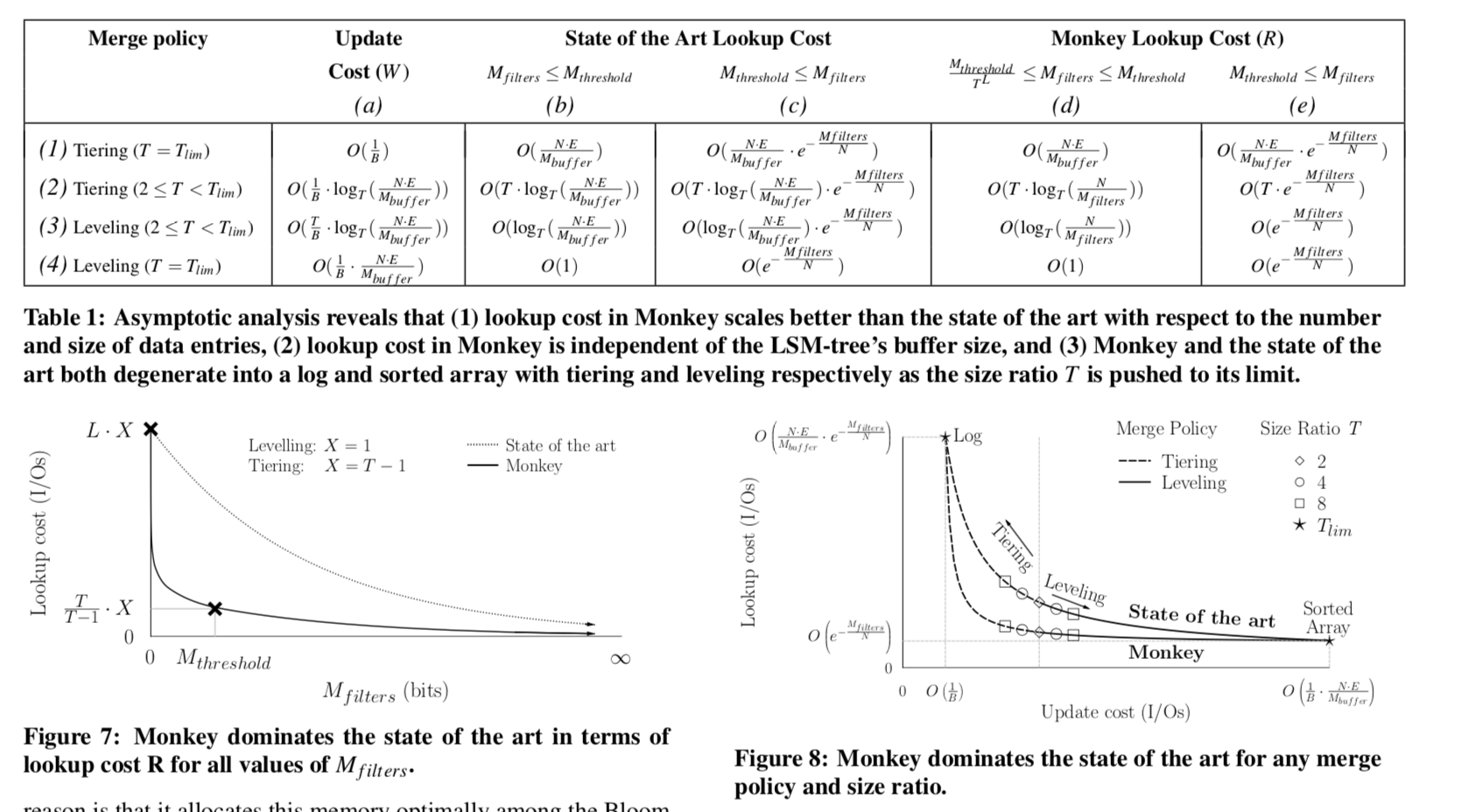
monkey-impact

论文的一个核心思想基本就是上面说的一些。论文中还有更加多的内容，比如分析内存在M-buffer和$M_{filters}$这里的处理、参数调整等的问题，可以参考[1].

0x05 评估

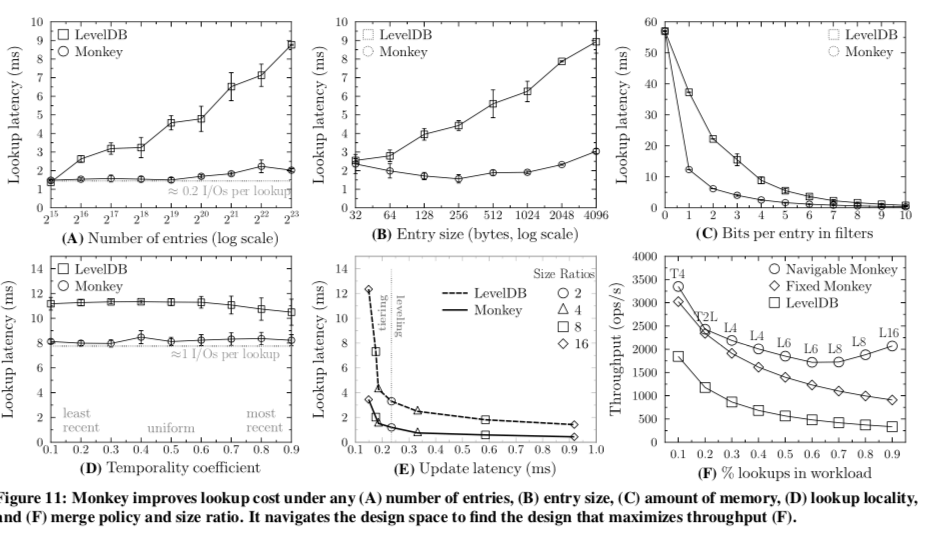
monkey-performance

参考

Monkey: Optimal Navigable Key-Value Store, SIGMOD 2017.