SuRF -- Practical Range Query Filtering with Fast Succinct Tries

SuRF: Practical Range Query Filtering with Fast Succinct Tries

0x00 引言

这篇Paper是SIGMOD2018得best paper。Succinct Range Filter (SuRF)是为了解决Bloom Filter不支持范围查找设计的。基与Succinct一种， Fast Succinct Trie (FST)，

Our experiments on a 100 GB dataset show that replacing RocksDB’s Bloom filters with SuRFs speeds up open-seek (without upper-bound) and closed-seek (with upper-bound) queries by up to 1.5× and 5× with a modest cost on the worst-case (all-missing) point query throughput due to slightly higher false positive rate.

0x01 Fast Succinct Tries

这里的一个基本的思路就是考虑到在Tries中，靠近root的node数量比较少但是访问的评论很高，相对的，远离root的node数据多但是访问的频率比较低。这里就是对这两种不同的node使用不同的编码方式，前者使用性能优化的LOUDS-Dense，而后者使用空间优化的LOUDS-Sparse。这些思路都是不是新的思路，在几十年前就出现了，这里可以看作是这些思路的一个综合性的应用。下面讨论的Tires的fanout为256，即一个byte。

surf-tire

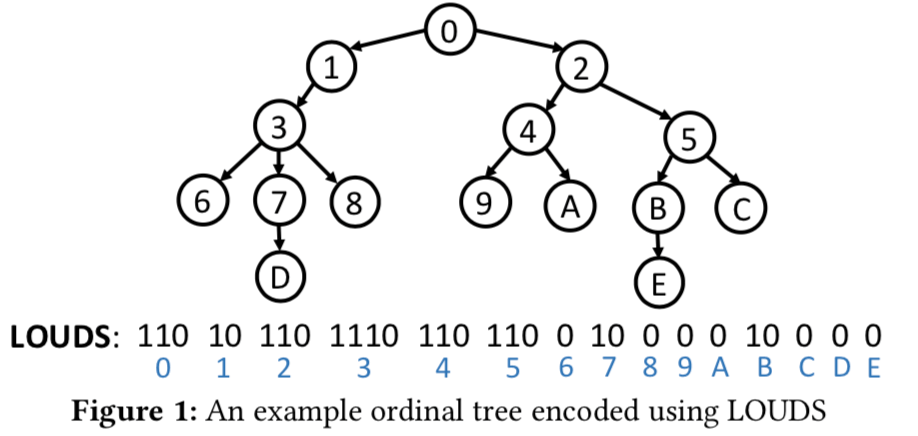
这里的一个重要的编码方式就是Level-Ordered Unary Degree Sequence(LOUDS)，它将tire的每一层编码为一个unary code。以下面的图为例，结点3有三个子节点，所以被编码为1110，为子节点数量个1加上一个0。整个tire按照BFS的遍历的方式来进行编码，最后得到整个tire的编码。

surf-louds

此外，在LOUDS里面，两个核心的操作就是select和rank。前者用于查找第i个0 or 1得位置，select_1(i)返回第i个1所在的位置，而select_0(i)则返回第i个0的。后者用于查找到指定位置i的1 or 0的数量，

 Given a bit vector, rank_1(i) counts the number of 1’s up to position i (rank_0(i) counts 0’s), while select_1(i) returns the position of the i-th 1 (select_0(i) selects 0’s). Modern rank & select implementations achieve constant time by using look-up tables (LUTs) to store a sampling of precomputed results so that they only need to count between the samples.

这里起始位置以0开始，这样有着以下的性质：

• Position of the i-th node = select0(i) + 1;

• Position of the k-th child of the node started at p = select0(rank1(p + k)) + 1;

• Position of the parent of the node started at p = select1(rank0(p));

LOUDS-Dense

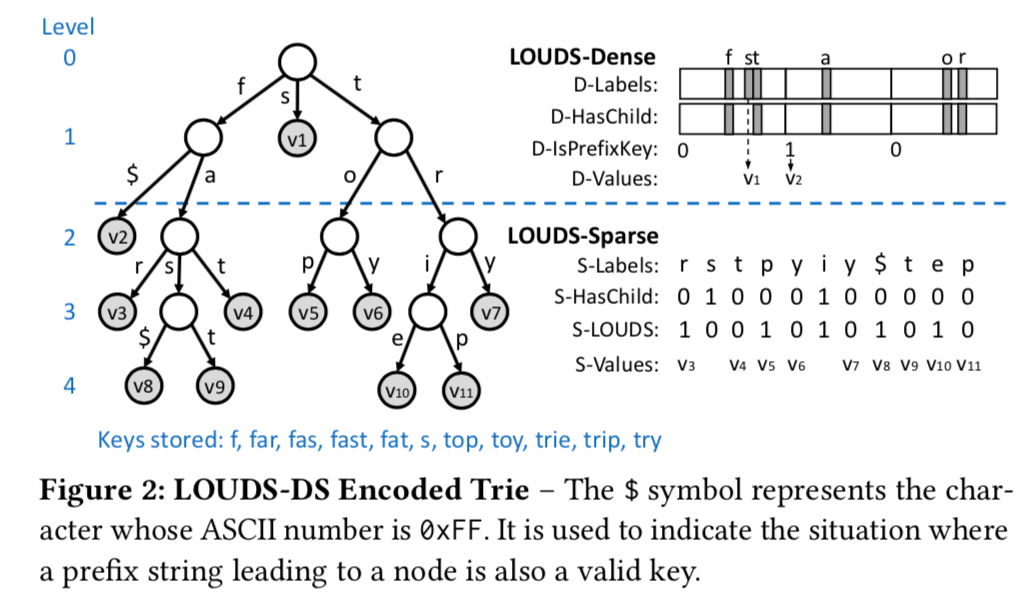
LOUDS-Dense节点有三个长度为256的bitmap和一个值组成的bytes的序列组成，在上面的图中有表示，

  • D-Labels，这个bitmap用于标识那一个位置存在分支。这里 0 <= i <=255。在最上面的图中，root分支存在f的子节点，所以在这个bitmap中，f对于的位置的标示就为1。

  • D-HasChild，这个bitmap也是256bits。这里用于表示这里是终止了还是存在子tire，

    Taking the root node in Figure 2 as an example, the f and the t branches continue with sub-tries while the s branch terminates with a value. In this case, the D-HasChild bitmap only sets the 102nd (f) and 116th (t) bits for the node.

  • D-IsPrefixKey，这个用于标识一个prefix是否也是一个存在的key。比如f在图2中也是一个key，而以f为prefix也存在。

  • D-Values，这里就是保存的值的序列，值的长度是固定的(不是这个序列长度固定)。值与位置的对应关系信息就是前面的几个bitmap。

这里的操作是这样的，

Tree navigation uses array lookups and rank & select operations. We denote rank1/select1 over bit sequence bs on position pos to be rank1/select1(bs, pos). Let pos be the current bit position in D-Labels. 

To traverse down the trie, given pos where D-HasChild[pos] = 1, D-ChildNodePos(pos) = 256 × rank1(D-HasChild, pos) computes the bit position of the first child node. 

To move up the trie, D-ParentNodePos(pos) = 256 × select1 (D-HasChild, ⌊pos/256⌋) computes the bit position of the parent node. 

To access values, given pos where D-HasChild[pos] = 0, D-ValuePos(pos) = rank1(D-Labels, pos) - rank1(D-HasChild, pos) + rank1(D-IsPrefixKey, ⌊pos/256⌋)-1 gives the lookup position.

解释：TODO。支持的几个基本的操作接口,

LOUDS-DS supports three basic operations efficiently:

• ExactKeySearch(key): Return the value of key if key exists (or NULL otherwise).

• LowerBound(key): Return an iterator pointing to the key-value pair (k,v) where k is the smallest in lexicographical order satisfying k ≥ key.

• MoveToNext(iter): Move the iterator to the next key-value.

LOUDS-Sparse

LOUDS-Sparse是一种节省内存的编码方式，使用2个bit和2个byte序列，

  • S-Labels，为一个byte序列，按顺序保证label数据。使用0xFF的特殊值来标识一个prefix也是一个合法的key，

      We denote the case where the prefix leading to a node is also a valid key using the special byte 0xFF at the beginning of the node (this case is handled by D-IsPrefixKey in LOUDS-Dense). For example, in Figure 2, the first non-value node at level 3 has ‘fas’ as its incoming prefix. Since ‘fas’ itself is also a stored key, the node adds 0xFF to S-Labels as the first byte. Because the special byte always appears at the beginning of a node, it can be distinguished from the real 0xFF label.

  • S-HasChild，为一个bit序列，这里同样用于标识是否存在子trie。

  • S-LOUDS，为一个bit序列，如果一个lalel是一个node中的第一个，那么这个标识就会被设置；

  • S-Values，为一个byte序列，这里和LOUDS-Dense的组织方式是一样的；

这里的操作是这样的,

Tree navigation on LOUDS-Sparse is as follows: 
to move down the trie, S-ChildNodePos(pos) = select1(S-LOUDS, rank1(S-HasChild, pos) + 1);

to move up, S-ParentNodePos(pos) = select1(S-HasChild, rank1(S-LOUDS, pos) - 1); 

to access a value, S-ValuePos (pos) = pos - rank1(S-HasChild, pos) - 1.

解释：TODO

Optimizations

  • 分段预计算，这就是将bitmap的分成固定大小的段，预先计算一下这里面的信息，这样的话实际计算的时候就只计算一个段里面的，

    Given a bit position i, rank1(i) = LUT[⌊i/B⌋] + (popcount from bit (⌊i/B⌋ × B) to bit i),

  • 使用popcount来加速一个bitmap中1数量的计算，使用SIMD来加速查找。使用数据预取减少Cache Miss带来的性能损失。

0x02 Succinct Range Filter

如果使用Fast Succinct Tries来做为Filter的话，FPR就是0，也就是说是完全精确的，但是这样的话内存的消耗也就大了。这里使用了下面的一些方式来减少内存的使用，

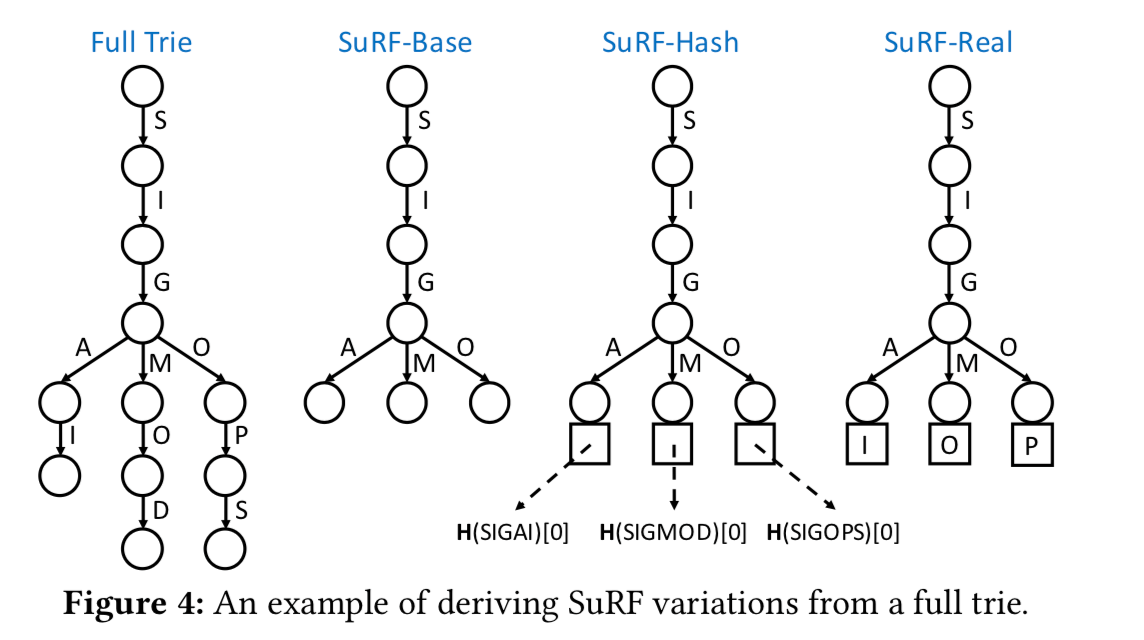
  • Basic SuRF，基本思路就是将一个保留一些字符串的公共前缀，剩余的部分只保留一个byte，其余的都扔掉。这样的做法简单，确定也很明显，就是FPR可能非常高，

    Instead of storing the full keys (‘SIGAI’, ‘SIGMOD’, ‘SIGOPS’), SuRF-Base truncates the full trie by including only the shared prefix (‘SIG’) and one more byte for each key (‘C’, ‘M’, ‘O’).
...
For example, if a SuRF-Base stores email addresses, query keys are likely of the same type. Our results in Section 4.2 show that SuRF-Base incurs a 4% FPR for integer keys and a 25% FPR for email keys.

  • SuRF with Hashed Key Suffixes，这里就是将前面的保留一个byte的换成hash值的几个bits，对于点查询效果是很好的，当这个bits程度为7的时候，这里的FPR就是1/2^7，缺点就是对范围查询的效果一般，

    The extra bits in SuRF-Hash do not help range queries because they do not provide ordering information on keys.

  • SuRF with Real Key Suffixes，这里将前面的hash值的几个bits换成了实际的suffixs，优点就是点查询和范围查询都能获利，缺点就是这个会提高FPR，特别是在实际的数据中，另外实际的数据往往存在相关性，而不是完全随机的，

    using real keys for suffix bits cannot provide as good FPR as using hashed bits because the distribution correlation between the stored keys and the query keys weakens the distinguishability of the real suffix bits.

  • SuRF with Mixed Key Suffixes，这里就是hash和read suffix的结合来

surf-filters

0x03 Benchmark

这里详细的信息可以参考[1].

参考

  1. Huanchen Zhang, Hyeontaek Lim, Viktor Leis, David G. Andersen, Michael Kaminsky, Kimberly Keeton, and Andrew Pavlo. 2018. SuRF: Practical Range Query Filtering with Fast Succinct Tries. In Proceedings of 2018 International Conference on Management of Data (SIGMOD’18). ACM, New York, NY, USA, 14 pages. https://doi.org/10.1145/3183713.3196931

Recent Posts

Emmmmmmm

Recommended Websites