Endurable Transient Inconsistency in Byte-Addressable Persistent B+-Tree
0x00 引言
今天继续来看一篇FAST2018上关于Btree的Paper,这篇Paper主要讲的是在PM(byte-addressable persistent memory)上面的B+-Tree上对数据Cache在CPU的Cache中和需要持久化保存到PM上面的一些问题。Paper主要就是提出了两个算法:Failure-Atomic ShifT(FAST,失败原子性挪动) ,Failure-Atomic In-place Rebalance (FAIR,失败原子性就地重平衡,不要在意这里的翻译(。ì _ í。))。这两种算法的使用使得使用8byte的store指令的时候让B+tree进入另外的一致的状态or或者是另外一种短暂的不一致状态,但是可以在读操作可以容忍这样的不一致的情况。这样就避免了为了保持一直的一致性而需要使用的COW、WAL之类的方法,从而提高性能,
• We develop Failure Atomic Shift (FAST) and Failure-Atomic In-place Rebalance (FAIR) algorithms that transform a B+-tree through endurable transient inconsistent states...
• We make read transactions non-blocking...
在PM上面实现PM在Paper中主要要解决下面两个问题:
- clflush and mfence,出现这个问题就是CPU Cache的问题,由于Cache的存在,现在常见的CPU都是不保证新的数据会被马上写入到内存中的,又可以还只是在Cache中。这Cache和DRAM配合工作时,这个不是上面问题,因为默认掉电后两个地方的数据都丢失了,而当Cache和PM配合使用时,这个就可能导致PM的一些持久化保存数据的特性得不到保证。clflush 和 mfence时x86上面用于刷新Cache相关的两条指令;
- 内存访问重排序,内存重排序可能导致持久化到PM上面的数据和程序写入数据的逻辑存在差别,进而可能导致一些问题。
0x02 Failure-Atomic ShifT (FAST)
这个算法的主要基于这样一个思想:在大部分的架构上面,如果store操作和load操作存在依赖关系,那么内存重排序的话就不会是随意的。在Btree的实现中,一种创建的操作就是在一个已经排序号的数组中插入一个新的元素。为了保证新的数据被持久化到PM里面,在TSO内存模型的架构上面,一般都会在写入操作的后面添加一个clflush的操作。而FAST的优化方式就是只在跨越Cache Line的时候才会进行clflush操作。这样在元素比较小的话就能够大大减少clflush操作的数量,在TSO的架构上面,由于满足了prefix constraint,这样处理的时候就简单了不少。这里必须保证刷新的Cache Line的顺序,不会被重新排序。由于store 操作和clflush操作可以被重排,这里需要mfence。这样带来的一个后果就是可能导致存在重复的数据,Paper中假设了实际上是没有重复的元素,这样的话遇到重复的直接忽略即可,
transactions ignore the key and continue to read the next key. This modification in traversal algorithm requires only one more compare instruction per each tree node visit, which incurs negligible overhead to transactions.
在比TSO更加松散的内存模型的机器上面,由于key, value给自shift操作的写可能被重新排序,这个时候就需要添加合适的mfence来保证正确性,在下面的伪代码中有表示,伪代码:
# Algorithm 1:
FAST insert(node,key,ptr)
node.lock.acquire()
if (sibling ← node.sibling ptr) != NULL then
if sibling.records[0].key < key then
– previous write thread has split this node
node.lock.release()
FAST insert(sibling,key,ptr);
return
end if
end if
if node.cnt < node capacity then
if node.search dir flag is odd then
– if this node was updated by a delete thread, we
– increase this flag to make it even so that
– lock-free search scans from left to right node.search dir flag++;
end if
for i←node.cnt−1;i≥0;i−− do
if node.records[i].key > key then
node.records[i + 1].ptr ← node.records[i].ptr;
mfence IF NOT TSO();
node.records[i + 1].key ← node.records[i].key;
mfence IF NOT TSO();
if &(node.records[i+1]) is at cacheline boundary then
clflush with mfence(&node.records[i+1]);
end if
else
node.records[i + 1].ptr ← node.records[i].ptr;
mfence IF NOT TSO();
node.records[i + 1].key ← key;
mfence IF NOT TSO();
node.records[i + 1].ptr ← ptr;
clflush with mfence(&node.records[i + 1]);
end if
end for
node.lock.release()
else
node.lock.release()
FAIRsplit(node,key, ptr);
endif
对于删除的操作,基本的思路和添加的操作是相同的,只不过是操作的顺序反过来的而已。
0x03 Failure-Atomic In-place Rebalance (FAIR)
这个算法主要的就是优化Btree结点的分裂操作,伪代码如下:
# Algorithm 2:
FAIR split(node,key, ptr)
node.lock.acquire()
if (sibling ← node.sibling ptr) != NULL then
if sibling.records[0].key < key then
node.lock.release()
FAST insert(sibling,key,ptr); return
endif
endif
sibling←nvmalloc(sizeof(node));
median ← node capacity/2
for i←median;i<nodecapacity;i++ do
FAST insert without lock(sibling, node.records[i].key,node.records[i].ptr);
endfor
sibling.sibling ptr ← node.sibling ptr;
clflush with mfence(sibling);
node.sibling ptr ← sibling;
clflush with mfence(&node.sibling ptr);
node.records[median].ptr←NULL;
clflush with mfence(&node.records[median]);
– split is done. now insert (key,ptr)
if key < node.records[median].key then
FAST insert without lock(node,key,ptr)
else
FAST insert without lock(sibling,key,ptr)
endif
node.lock.release()
–update the parent node by traversing from the root.
FAST internal node insert(root,node.level+ 1,sibling.records[0].key,node.sibling ptr);
基本的操作步骤如下面的图所示,这里也使用了前面的可以容忍出现重复数据的方法。拷贝被分裂结点的操作最先进行,拷贝完成之后,原子性地置原结点中间的元素Pointer为NULL,,然后再去做实际的删除操作。在此之前,新到的结点里面的数据都不会被使用。另外还要处理的就是父结点的可能出现的不一致的状态,下面的这个图的后面三个字图表示出了使用的方法,基本的思路就是使用sibling的指针和容忍重复的数据。
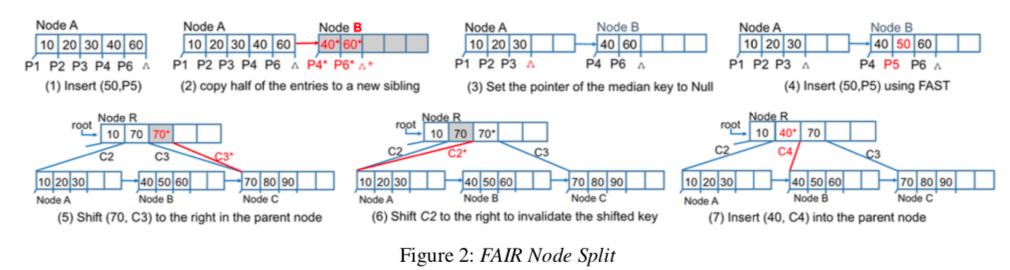
对于结点的操作同理,只是操作相反。
0x04 无锁查找
前面的算法保证了部分更新的时候读取操作也能返回正确的结构,这样这里的实现就相对比较简单了。为了实现lock-free的查找,查询操作的顺序必须沿着同样的方式,要和shift操作移动的顺序相反,
while a write thread is shifting keys and pointers to the right, read threads must access the node from left to right. If a write thread is deleting an entry using left shifts, read threads must access the node from right to left.
方向的确定使用一个计数的flag的值,提交为偶数,删除的时候为奇数。这样的限制也就导致了不能使用二分查找。但是如果这个结点的大小不大的话,这个还是没有多大的影响的。另外一个问题,由于方向的不确定性等原因,这个查找算法没有使得两个事务之间序列化,这样就可能导致 phantom reads 和 dirty reads,比如一个事务准备添加10和20两条基本,另外一个事务的操作是范围操作,查找的事务可能看到了其中的一个,耳目看到另外一个。在一些情况下,比如数据库,需要处理这种情况的话,可以使用其它的方法来解决,比如key range locks, snapshot isolation, 后者是 multi-version schemes等。
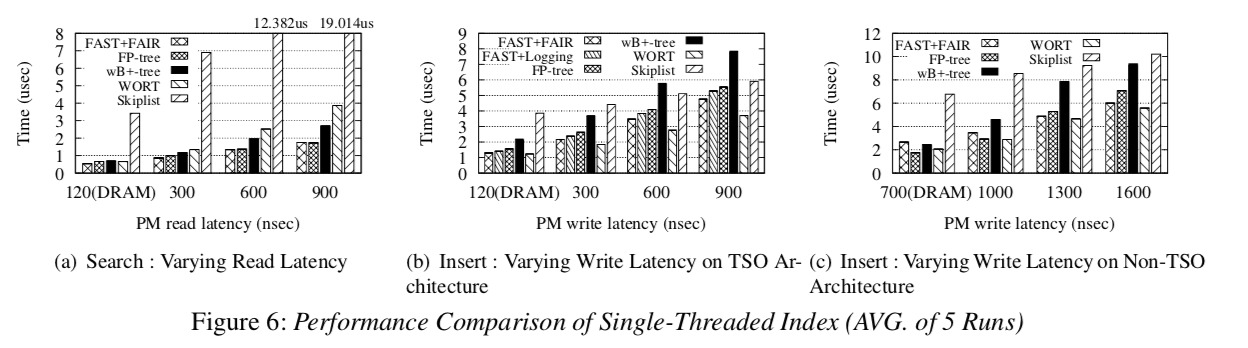
0x05 评估
详细信息参看[1]
参考
- Endurable Transient Inconsistency in Byte-Addressable Persistent B+-Tree, FAST’18.
