Copa -- Practical Delay-Based Congestion Control for the Internet

Copa: Practical Delay-Based Congestion Control for the Internet

0x00 引言

Copa也是一个基于delay的拥塞控制的算法，它有3个基本的idea，

在 Markovian(马尔可夫) packet arrival 模型下面，最优化的吞吐和延迟的目标发送速率为1 / (δ*dq)，这里的dq为测量到的排队延迟；
Copa根据目标发送速率来调整窗口，即使在系统中存在诸多不稳定的因素下，它也能快速收敛到一个正确的公平的速率；
第3个idea使用用来解决基于delay的算法在基于丢包的算法目前太“君子”的问题，比如Vegas就存在这个问题。Copa的解决方法是根据delay的变化来对参数δ进行additive-increase/multiplicative decrease(AIMD)的变化；

Copa能和Cubic在一个环境下比较好的共同存在，这个比BBR、PCC做的好(也应该包括Vegas)。

0x01 基本思路

Copa这里的目标发送速率是1 / (δ*dq)，dq的含义如前面所言，这样1 / δ的含义就是MTU尺寸包的量。Copa中cwnd的含义和一般的含义相同。在每个ACK达到的时候，发送方使用λ = cwnd/RTTstanding来估计目前的发送速率，这里的RTTstanding是在最近的一个时间窗口 τ(τ=srtt/2, srtt就是rtt的估计，和一般的方法一致，选择这样一个时间段内是为了反之ACK compression或者是网络抖动带来的影响)内观察到的最小的值。Copa使用dq =RTTstanding−RTTmin来计算dq，RTTmin是在一段比较长时间内观察到的最小值(在Copa中使用了一个小于10s的值)。如何利用前面计算目标速率的方式，在超过了目标速率之后，就减少cwnd，反之增加cwnd。Copa发送方的在ACK达到之后的处理逻辑，

更新dq的计算方法更新dq的值，同时更新srtt的估计；
根据目标速率的计算公式计算出此时的目标速率λt；
如果当前使用的目标速率λ = cwnd/RTTstanding小于等于λt，更新cwnd的值为cwnd = cwnd + v/(δ*cwnd)，这里的v是一个速率参数。反之为cwnd = cwnd - v/(δ*cwnd)，也就是说一次变化的delta为v/(δ*cwnd)；
参数v在开始的时候初始化为1，这里的思路和前面的PCC，PCC-Vivace的思路相似。都是加速收敛的方法，在一个发送上面多走了几次，就加大v的值(每次double)，方向变化了重新设置为1。在开始的时候要特殊处理，只有在保持了同一方向的变化3RTTs时才应用这个方法，
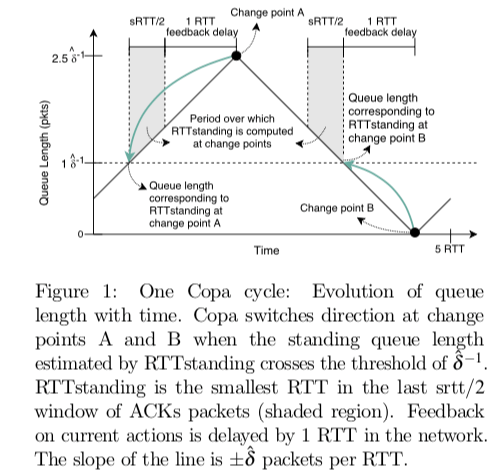
```
However, start doubling v only after the direction has remained the same for three RTTs. Since direction may remain the same for 2.5 RTTs in steady state as shown in figure 1, doing otherwise can cause v to be >1 even during steady state. In steady state, we want v = 1.
```

在连接刚刚建立的事，也是使用slow-start的方式，直到λ大于λt。

处理Buffer-Filling问题

这个即Copa算法的第3个idea，使用 δ处理太“君子”的问题。初始的时候 δ设置为0.5。如果Copa观察到在5个5 RTTs内RTTs没有很大的变化，就认为目前没有什么排队现象，

We estimate “nearly empty” as any queuing delay lower than 10% of the rate oscillations in the last four RTTs; i.e., dq < 0.1(RTTmax − RTTmin) where RTTmax is measured over the past four RTTs and RTTmin is our long-term minimum as defined before.

如果Copa判断方式了排队的现象，则进入competitive mode。在这个模式在 δ的变化方法可以根据情况设置。在Paper中的实现中利用的事基于包发送成功与否的AIMD策略。

copa-cycle

0x03 Justification of the Copa Target Rate

Copa的目标速率为1 / (δ*dq)。Copa使用的效用函数为(Copa的目标为是U取最大值)。(Why???,¯_(ツ)/¯) \(\\ U = \log \lambda - \delta\log d,这里\lambda为吞吐，d为延时,\\ 对于流i有 U_i = \log\lambda_i - \delta_i\log d_s,这里的延迟为"交换机延迟“, d_s = d_q + \frac{1}{\mu}, \\ 总的吞吐为\lambda = \sum\lambda_i，在M/M/1的排队模型下面，平均等待时间为\frac{1}{\mu - \lambda}(不知道怎么算出来的), \\ 对于 U_i,有 U_i = \log \lambda_i + \delta_i\log(\mu - \lambda_i - \sum_{j \neq i}\lambda_i),对其求\lambda_i的偏导，有\delta_i\lambda_i+\sum\lambda_i = \mu, 且二阶偏导<0. \\ 使偏导为0,即有\lambda_i(1+\delta_i) + \sum_{j\neq i}\lambda_i = u，唯一解为\lambda_i = \frac{u}{\delta_i(\sum(1/\delta_i)^{-1} + 1) }\) 对于前面所说的τ，有 \(\\τ_i = \frac{1}{\lambda_i}, 根据d_s = \frac{1}{\mu - \lambda}, τ_i = \delta_i\cdot d_s = \delta_i(d_q + 1/\mu)\) ¯_(ツ)/¯ , (´･ω･`)

0x04 评估

这里的详细信息可以参看[1].

参考

Copa: Practical Delay-Based Congestion Control for the Internet, NSDI’18.