A General-Purpose Counting Filter: Making Every Bit Count

0x00 引言

这篇Paper描述了一种Quotient Filter的优化思路。Quotient Filter是一种功能类似于Bloom Filter但是思路存在很大差别的Approximate Membership Query (AMQ)数据结构。Quotient Filter的基本思路如下，

• 在Quotient Filter中，使用一个hash函数的计算一个元素一个hash值，使用这个值的一部分的bits定位一个slot，剩下的部分称之为商，保存到这个slot中。slot中除了这个商之外，还保存另外三个bit: 1. is occupied，如果这个slot就是保存的商根据hash值应该保存的位置时设置为1。因为在这里slot中保存的值可能被移动。2. is_continuation，添加元素的时候如果slot已经被占用，则根据商的大小决定移动元素，形成从小到大的余数排列，这个bit用来记录这些记录是否连续。这些元素称之为run or cluster。3. slot中保存的商时被移动过来的设置为1。
• 在查询的时候根据hash值找到对应的slot，如果这个slot不是对应的元素，且存在run/cluster，则往后查找，直到达到run/cluster末尾 or 商更大。Quotient Filter类似于linear probing的hash。其优点是缓存友好性优于Bloom Filter，但是可能在占用率高的时候性能比较差。

0x01 基本思路

Rank-And-Select-Based是Succinct数据结构中使用的一种策略，这里提出了Rank-And-Select-Based Quotient Filter使用了类似的策略来优化Quotient Filter。其基本的思路如下，这里不是使用3个标记为，而是两个，第一个occupieds标记是否有一个值定位到了这里，另外一个为runneds，用来标记一个run的结尾。这里定义了两个运算，第一个Rank(B, i)返回bit vector B中到i位置为止的bit为1的数量，Select(B, i)返回第i个bit为1的index。这样在其中查找一个元素是否存在可以用如下的方式：第一个先查询occupieds是否存在，没有就是返回0。存在则根据RANK定位在slot中能够到达的最大的位置，用 t ← RANK(Q.occupieds, b) 、 l ← SELECT(Q.runends, t)两个式子计算出来。下面就是在这个可能的范围内查找是否有对应的remainder。有则返回true，否则返回false。这个的设置在分析FPR的时候会比Bloom Filter难上不少。其添加的过程也比较复杂[1]。这里实际在计算Rank和Select的时候会使用一些特殊的CPU指令来加速。

function MAY_CONTAIN(Q, x) 
  b ← h0(x)
  if Q.occupieds[b] = 0 then 
    return 0
  t ← RANK(Q.occupieds, b) 
  l ← SELECT(Q.runends, t) 
  v←h1(x)
  repeat
    if Q.remainders[l] = v then 
      return 1
    l←l−1
  until l < b or Q.runends[l] = 1 
  return false

另外Paper中还描述了如何为此添加Counter的方式。emmm看起来一点都不好玩。

0x02 评估

这里的具体信息可以参看[1].

Persistent Bloom Filter: Membership Testing for the Entire History

0x10 引言

这篇Paper突出的Filter的类似很有意思。一般的Filter表达的是一个元素是否存在一个集合之中。Persistent Bloom Filter则引入了另外一个维度，可以处理一个时间段内一个成员是否存在一个对象之中。在提出Persistent Bloom Filter之前，可以利用现在已经存在的一些算法来实现查询一个时间范围内一个元素是否出现过。利用单的Bloom Filter，这里只需要做两点改变，1. 在添加的时候不能只用元素本身来计算若干个hash值，还需要加上这个元素出现的时候，即使用hash(entry, timestamp)来计算一个hash值。在查询的时候，使用query(x, s, e)接口，即x在[s，e]的时间段内有没有出现过。查询就需要对于这个时间范围内的每个时间戳计算hash，查询是否存在。这里查询次数复杂度为O(T)，和查询时间范围的相关；另外的一种方式是利用persistent sketch，出现在论文[4]中。

0x12 基本思路

PBF-1

PBF-1的思路类似于线段树，一种支持范围处理的一种数据结构。基本的思路如下图，假设时间范围的上界为T，且为2的次幂，如果不是也很容易处理为2的次幂。这样每个层将上一层的一个区间划分为2，第一层的区间数量为1，这样形成的是一个高度为log(T)的树形结构，树的形状是固定的。这个思路就是一个线段树的思路。这里的每个区间为一个Bloom Filter，不同level的Bloom Filter的大小不同。最后一层，就是一个一般的Bloom Filter。在这样的结构中查询一个元素是否在一个区间中出现过，使用如下的策略: 1. 在第i层的时候，如果当前的区间超出了要查询区间的表示访问，比如下图中l=0是[1，8]超出了要查询的[1，6]的区间，则查询下一层包含这个区间某各部分的区间，2. 如下图，在第二层的时候，b2，b3区间都包含了要查询的区间，而b2都在要查询的区间范围内，则直接查询b2即可，而对于b3，由于又超出了要查询的区间则递归查询下一层。3. 查询存在的话，查到一个结果就可以直接返回。至于这样的结构如何构建，在知道了如何查询之后也很明显了。

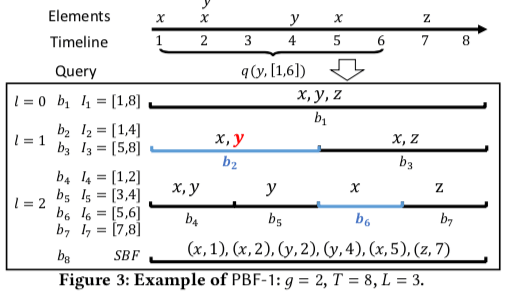
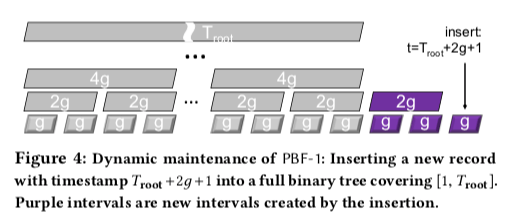
上面的例子是一个时间范围静态的例子。在streaming类型中，元素到来的时间戳逐渐增加，这样的话可以使用逐渐构建这个tree的方式，每隔g个时间创建一个g类型的节点，每隔2g的时间创建一个2g类型的节点。在创建2g类型的Bloom Filter的时候，可以直接使用下面g bitor的方式构造2g。

PBF-2

PBF-1算法简单，性能也不错。不过PBG-1的缺点是使用太多的Bloom Filter，造成的比较大的space overload。PBF-2算法就是为了解决这个问题，PBF-2算法中每个level只会使用一个Bloom Filter。每层将一个时间范围的元素组织为一组，这个时间范围的粒度根据不同的level设置，上一层为下一层的两倍。这里实际上就是将一个Bloom Filter拆分为多个子段的逻辑。整体的算法区别很小。

0x13 评估

这里的具体信息可以参看[2].

##Morton Filters: Faster, Space-Efficient Cuckoo Filters via Biasing, Compression, and Decoupled Logical Sparsity

0x20 引言

Morton Filters这篇Paper是关于Cuckoo Filter的一个改进，包括使用空间方面的改进、内存访问的优化以及查找的时候需要使用的hash函数数量的改进等，

 Like CFs, MFs support lookups, insertions, and deletions, but improve their respective throughputs by 1.3× to 2.5×, 0.9× to 15.5×, and 1.3× to 1.6×. MFs achieve these improvements by (1) introducing a compressed format that permits a logically sparse filter to be stored compactly in memory, (2) leveraging succinct embedded metadata to prune unnecessary memory accesses, and (3) heavily biasing insertions to use a single hash function.

0x21 基本思路

Morton Filter的基本思路就体现在下图中。它将Cuckoo Filter中多个Bucket的信息以一种压缩的方式保存到一个Block。在实际的一些数据中，Cuckoo Filter中的很多Bucket都是没有满的，这样就会浪费不少的空间。另外一个这样压缩保存的方式使得数据更加紧凑，多余一些查找占比比较高的workload缓存更加优化，也就会有更好的性能。 Morton Filter中一个Block分为三个部分，一个FSA，用来保存Cuckoo Filter中Bucket中的数据，另外的一个FCA，用来保存FSA中保存在前面Bucketfingerprint的数量的前缀和。这样是为了在压缩保存的状态下吗定位一个原来Bucket里面数据的位置。OTA用来保存是否overflow的信息，在没有overflow的情况下，就可以只使用一个hash来查找，避免了一些不必要的查找操作。也就是优化中的第三点，其实也没有特别的。Morton Filter中使用两个hash函数，一个称之为primary hash function，另外一个为secondary hash function。使用下吗的策略定位一个位置， \(H_1(K)=map(H(K),n), \\ H_2(K)=map(H_1(K),(-1)^{H_1(K)\&1}\cdot offset(H_f(K)),n) \\ H'(\beta,H_f(K))=map(\beta+(-1)^{\beta\&1}\cdot offset(H_f(K)),n)\\ offset(F_x)=[B+(F_x\%OffRange)]|1\) H为一种hash函数，map(x,n)将x映射到0到n-1的一个值，而H_f(K)为K的fingerprint。根据上面的计算方式，逻辑上将bucket范围奇偶两个部分。这样可以在不知道K的情况下计算H’，和重新映射K的fingerprint。

在这样的设计中，一些基本的操作如下，

• 查找，首先根据H_1计算出一个primary bucket的索引，根据这个索引去对应的Block查找，如果存在 or 不存在且没有overflow则直接返回。如果没有且overflow了，则需要查找第一个候选的位置。

• function likely-contains(MF,Kx) 
    Fx=HF(Kx)
    glbi1 = H1(Kx)
    block1 = MF.BlockStore[glbi1/B] 
    lbi1 = mod(glbi1, B)
    match = table read and cmp(block1, lbi1, Fx)
    if (match or OT A bit is unset(block1, lbi1)) then
      return match 
    else
      glbi2 = H2(Kx)
      block2 = MF.BlockStore[glbi2/B]
      lbi2 = mod(glbi2, B)
      return table-read-and-cmp(block2, lbi2, Fx)
  

• 添加，添加的查找要稍微复杂一些，因为要处理溢出的问题和处理Block中FCA信息的问题。在添加的时候，FSA中间添数据需要对左边的数据进行移动的操作。如果出现overflow的情况，处理的方式和Cuckoo Hash中的方式类型，也会存在一些Cuckoo Hash中存在的问题，比如驱逐操作进行次数过多，也可能存在循环驱逐等。这里还需要设置OTA里面的overflow的信息。

• 在两个基本的操作之外，Morton Filter还可以支持删除操作，定位需要删除数据的位置和查找操作的方式相同。在删除的时候，数据的移动操作和添加的时候想法，同样需要更新FCA的信息。

参考

1. A General-Purpose Counting Filter: Making Every Bit Count, SIGMOD ‘17.
2. Persistent Bloom Filter: Membership Testing for the Entire History, SIGMOD ‘18.
3. Morton Filters: Faster, Space-Efficient Cuckoo Filters via Biasing, Compression, and Decoupled Logical Sparsity, VLDB ‘18.
4. Persistent Data Sketching, SIGMOD ‘15.
5. Vectorized Bloom Filters for Advanced SIMD Processors, DaMoN’14.