PCC: Re-architecting Congestion Control for Consistent High Performance

0x00 引言

PCC发表在BBR算法之前，虽然两者之间存在着很多的差异，但也在很多方面的思路是类似的。一个基本的想法就是不能简单地认为丢包了就是一定发生了阻塞。BBR使用的方法是测量线路这个“管子”的容量来实现拥塞控制。而PCC则是通过改变发送速率之后出现的时间来判断线路目前的情况。Paper中的PCC算法的数据很不错，而且能够适应的环境非常广泛，这个也是一个很大的优点，

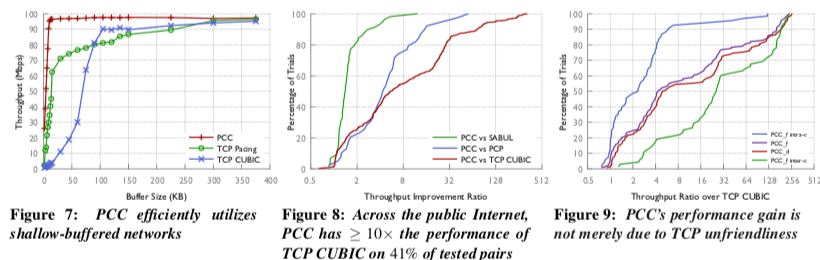
PCC achieves consistent high performance and significantly beats specially engineered TCPs in various network environments: 
(a.) in the wild on the global commercial Internet (often more than 10× the throughput of TCP CUBIC); 
(b.) inter-data center networks (5.23× vs. TCP Illinois);
(c.) emulated satellite Internet links (17× vs TCP Hybla); 
(d.) unreliable lossy links (10−37× vs Illinois); 
(e.) unequal RTT of competing senders (an architectural cure to RTT unfairness); 
(f.) shallow buffered bottleneck links (up to 45× higher performance, or 13× less buffer to reach 90% throughput); 
(g.) rapidly changing networks (14× vs CUBIC, 5.6× vs Illinois). 
(h.)PCC performs similar to ICTCP in the incast scenario in data centers.

0x01 基本思路

... based on live experimental evidence, avoid- ing TCP’s assumptions about the network. PCC sends at a rate r for a short period of time, and observes the results (e.g. SACKs indicating delivery, loss, and latency of each packet). It aggregates these packet-level events into a utility function that describes an objective like “high throughput and low loss rate”. The result is a single numerical performance utility u. 

PCC的基本的基本思路来自下面几个ideas：

• 对于一个流f，如果f是导致阻塞的主要原因，那么它就应该减小发送的速率；
• 在高high-BDP(网络上的Buffer容量很大的情况)，可能收到shallow buffer的影响而导致丢包，这个时候只要稍微降低发送速率即可；
• 如果阻塞的原因是路线上面其它的发送速率更加高的流导致的，那么这个流f就不要降低发送速率，让那个速率更加高的降低；
• 有些丢包是路线本身的一些原因or就是随机的未知情况(某些运营商在某些路线上随机丢包，23333)，而和阻塞没有什么关系，这个时候还是可以继续增加发送速率；

有了上面的这几个ideas，接下来的问题就是如何探明这些情况or如何判断目前大概是个什么情况了。

0x02 实现

PCC将时间切分为连续的 monitor intervals (MIs)，MI的程度通常为1到2个RTT的时间。PCC在一个MI内，选在一个发送 的速率r，在这个MI内都以这个速率发送，在大约一个RTT之后，发送方会看到SACK，PCC将这些ACK的信息转换了性能评价的指标如吞吐、丢包率和延迟。这些指标通过一个utility function函数计算一个效用值，使用u表示。在一个其实的速率r下，后面PCC会尝试(1+ε)*r 和 (1−ε)r的速率。PCC会朝着让效用值更加高的方向移动。为了减少一些测试噪音，PCC不是使用在两个MI内测试的方法，而是在四个MI内已随机的顺序测试两种不同的速率。如果在两边都得到更加高的效用值，PCC选择其中的一个值来作为下次的发送效率。这种方式将发送速率的方差降低了35%。

公平性和收敛性

PCC选择的效用函数为，在有n个发送者的一个网络中，网络最大的带宽为C， \(\\ 每一个发送者i的效用函数为 u_{i}(x_{i}) = T_{i} \cdot Sigmoid_{\alpha}(L_{i} - 0.05) - x_{i}\cdot L_{i},\\ L_{i}为i观察到的丢包率，T_{i} = x_{i}(1-L_{i})为发送者i的带宽，其中Sigmoid_{\alpha}(y) = \frac{1}{1 + e^{\alpha y}}, \alpha > 0;\) 可以证明存在以下的结论[1]，

• 到a >= max{2.2(n − 1), 100}的时候，最终的稳定状态都是相等的，即x1’ = x2’ = … = xn’。即PCC保证了公平性；
• 对于每一个发送者，发送速率会汇聚在(x’(1 − ε )^2 , x’(1 + ε )^2 )，x’为发送的稳定状态的值。

PCC的使用不需要路由器的支持，不需要对现在协议改动，也不需要接收方的改动。

性能监控

监控模块会记录在每一个MI内发送的数据包的一些信息，在之后接受到SACK的时候可以用来计算性能指标数据。在下面的图中，监控数据包在时间T0到T0+Tm的范围内。为例确保有足够的数据包，这里的Tm设置为max{发送10个包的时间，一个在[1.7,2.2]中的均匀分布的随机的倍数乘以RTT}。PCC发送数据包不会等待性能结果，而是会继续发送。

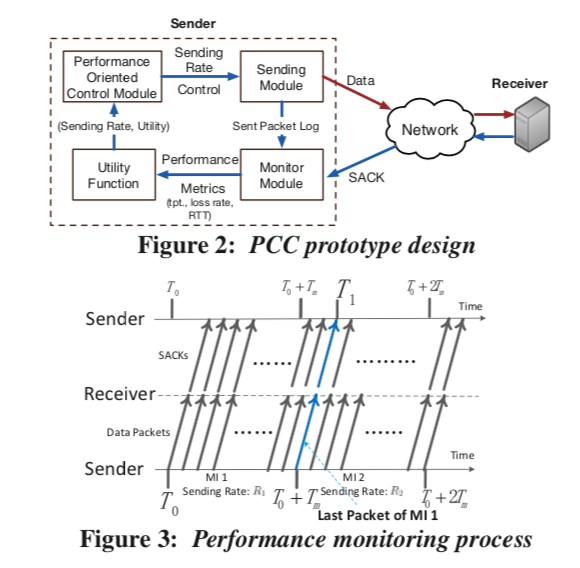
控制算法

PCC这里的控制算法分为3步，

• Starting State，启动状态，启动的发送速率设置为 2 · MSS/RTT，然后在之后的每一个MI内发送速率加倍。PCC终止启动阶段不是以包丢失来确定的，而是计算的效用值下降的时候；

• Decision Making State，这里阶段工作的思路就如下面的描述。PCC选择4个MI，分为2组(随机)，一组以r(1 + ε )速率发送，另外一组以r(1 - ε )发送，之后计算出来的效用值记为Ui+,Ui-，如果Ui+ > Ui-，新速率设置为r(1 + ε )，反之设置为r(1 - ε )。但是U1+ U2+和U1-，U2-的大小比较不一致，则保留在当前的速率。同时设置ε = ε +εmin，但是最大不同超过εmax。这里使用 εmin = 0.01， εmax = 0.05；

• Rate Adjusting State，这里可以理解为在一个速率方向一直增长的话，那么现在的发送速率里饱和的点还有一段距离，这样就可以把步子“迈开一点”。

   Assume the new rate after Decision Making is r0 and dir = ±1 is the chosen moving direction. In each MI, PCC adjusts its rate in that direction faster and faster, setting the new rate rn as: r_{n} = r_{n−1} · (1 + n · εmin · dir). However, if utility falls, PCC reverts its rate to r_{n−1}  and moves back to the Decision Making State.
  

0x03 评估

这里可以参看[1]

PCC Vivace: Online-Learning Congestion Control

0x10 引言

这篇文章是上面的Paper的后续吧，作者也几乎是相同的。PCC Vivace可以看作是在PCC的基础之上的改进。和前面的PCC相比，PCC Vivace有这些的不同，

• 效用函数中加入了延迟，缓和了bufferbloat(缓存过满)的问题；
• 不同的发送者可以使用不同的效用函数；
• 对一般的TCP更加友好；
• 速率控制更加快速收敛，对网络的变化反应更加敏感；

0x11 基本思路

PCC Vivace的效用函数为， \(\\ u(x_{i}, \frac{d(RTT_{i})}{dT}, L_{i}) = x_{i}^t - bx_{i} \frac{d(RTT_{i})}{dT} - cx_{i}\cdot L_{i}, \\where 0<t<1,b≥0,c>0,x_{i}是发送速率,L_{i}为丢包率, \frac{d(RTT_{i})}{dT} 为MI内RTT 变化的梯度; b,c,t为常数;\) 另外， PCC Vivace同样也是公平的，最终会收敛(收敛的速度比PCC更加快)，而且可以通过设置参数来设置对丢包的忍受程度，另外就是支持不同的资源的分配。这里设计到比较多的数学证明[2]。

0x02 速率控制

PCC Vivace同样使用在几个连续的MI中测试r(1 + ε )和 r(1 − ε )的方法，不过设置下一个速率的时候使用的梯度的方法。设这个两个测试到的效用函数为u1,u2， \(\\ \gamma = \frac{u_1 - u_2}{2\varepsilon r}, r_{new} = r + \theta_0\gamma\) 这里的PCC Vivace引入了confidence amplifier的概念，和PCC逐渐迈开步子的思路是一致的。这里就是一个函数m(n)，n为在同一个方向决策的次数，这里每次的变化就变成了, \(\\ r_{new} = r + m(n)\theta_0\gamma\) 这个会在增长方向变化的时候归位。

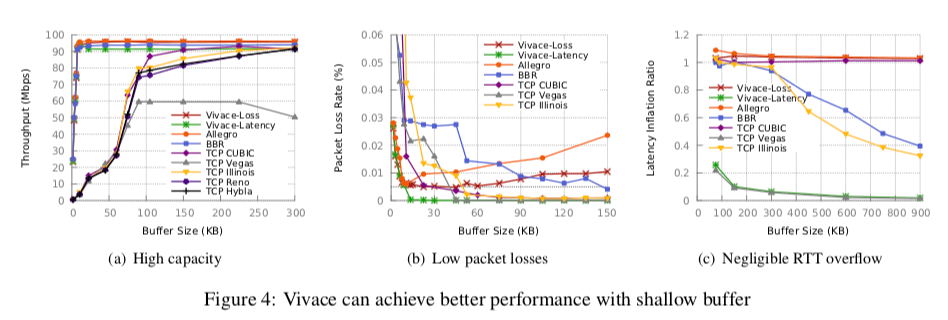
0x03 评估

这里的具体的信息可以参看[2],

参考

1. M. Dong, Q. Li, D. Zarchy, P. B. Godfrey, and M. Schapira. PCC:Re-architecting Congestion Control for Consistent High Performance.In NSDI, 2015.
2. M. Dong, T. Meng, D. Zarchy, E. Arslan, Y. Gilad, B. Godfrey, and M. Schapira. PCC Vivace: Online-Learning Congestion Control. In NSDI, 2018.