Join-Idle-Queue: A Novel Load Balancing Algorithm for Dynamically Scalable Web Services

0x00 引言

Join-Idle-Queue算法很简单，设计地也很巧妙。JIQ面向的主要就是Web Servers的环境，不过应该也可能应用到其它的很多环境。它的一个基本思路是尽量减少Dispatcher(即负责分发任务的机器)和Processor(即处理任务的机器)之间的交互，JIQ通过另外的一个Idle Queue将两者之间的交互解耦。Processor在处理完任务之后将自身的信息添加到某些DIspatcher对应的Idle Queue中，表明自己可以接受新的任务，所以算法称之为Join-Idle-Queue。

0x01 算法

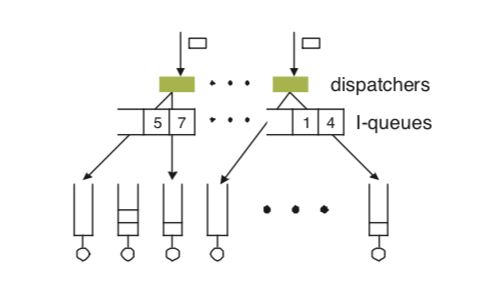
JIQ算法的基本示意如下图，Dispatches和后端的服务器之间通过中间的I-queues来通信。每一个Dispatchers会对应一个I-queues。JIQ的负责均衡主要有两个部分，

• Primary load balancing，Dispatcher在有任务需要分发的时候，询问其对应的I-queue，这个queue如果存在数据，则移除其中的第一个Processor。然后将其分发给对应的Processor。如果这个queue里面没有数据，则选择一个随机的Processor分发。在一个Processor处理完它的任务的或者是接近处理完之后，它将其它的信息添加到一个I-queue中。
• Secondary load balancing，这里主要就是处理一个Processor变成空闲的之后，它如何选择I-queue的方法。这里就使用之前的一些方法，比如随机选择一个后者是挑选几个选择其中队列最短的。

0x02 评估

这里的具体信息可以参看[1],

DistCache: Provable Load Balancing for Large-Scale Storage Systems with Distributed Caching

0x10 引言

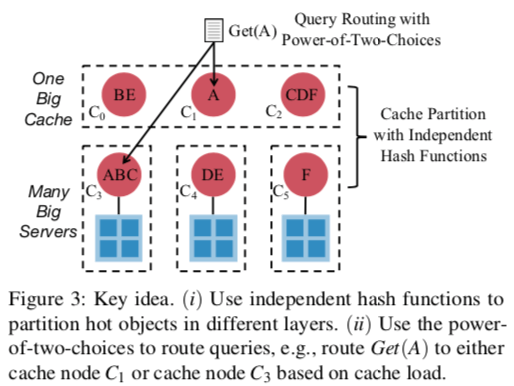
DistCache是一种为存储系统设计的一种缓存方式。它的基本方式是使用一个两层的Cache结构，不同的层使用不同的Hash函数，用于将热点的数据尽可能的分散到不同机器上面，

0x11 基本思路

在之前的一些解决方案中，常见的两种方式是Cache分区和Cache复制。对于前者的缺点就是处理热点Key的时候不能很好地分散这些请求，而后者的缺点在于Cache一致性的处理比较困难，整体系统的复杂度也更加大。而DistCache则采用了上图中的设计，在不同的层使用不同的Hash函数尽可能的去分开热点数据的查询。另外，在选择那个缓存节点处理查询的时候，就采用了简单有效的 power-of-two-choices的方法。就是随机找两个选择其中load更加小的。另外文中还有一大堆对这个方法具体情况的分析[2]。

Paper中实现了类似于NetCache的一个基于交换机的DistCache的一个实现。上面架构是在一个two-layer leaf-spine架构中的数据中心网络中的一个实现。在这个实现中，会有一个Cache Controller管理处理缓存交换机、处理设备故障。Cache交换机负责缓存热点数据，同时负责分发它的load的信息，这个load的状态会用于如何路由这个查询。于客户端相连的ToR交换机负责处理查询路由的问题(使用power-of-two-choices的测量)。后端的存储节点可以就是一个一般的KVS。下图是一个处理流程的例子。S6与客户端相连，S6使用power-of-two-choices选择了S1 S3，根据负载信息从中选择一个。缓存命中的时候直接返回即可。缓存缺失的时候，操作会被直接转发到存储节点。

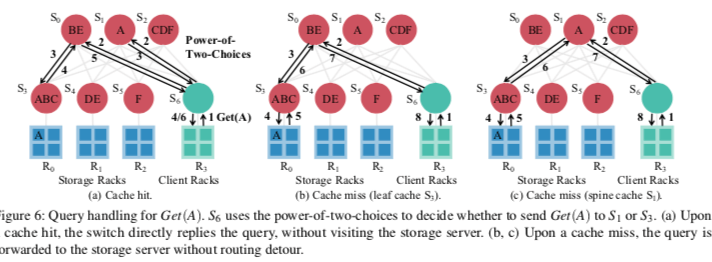
这里另外要处理的一个比较重要的问题就是缓存一致性和缓存更新的处理。对于缓存一致性，它使用了一种一般两阶段更新的方式，就是会先处理缓存让其失效，然后在更新操作，

 To apply the protocol to our scenario, after receiving a write query, the storage server generates a packet to invalidate the copies in the cache switches. The packet traverses a path that includes all the switches that cache the object. The return of the invalidation packet indicates that all the copies are invalidated.

Paper中这里好像有一个问题没有提到如何处理，就是在一个Cache节点里面的数据被值为无效之后，它回复了存储节点。存储节点就以为这个Cache节点的缓存已经失效了。不过这个时候，一个客户端新的请求来了，刚好请求了相同的Key，而且刚好经过这个节点，这个节点去存储节点读取数据。如果这个时候存储节点的数据还没有更新(比如存储节点还在处理其它节点的失效的问题)，这个时候这个缓存节点就是缓存了之前的数据，之后存储节点上面的数据被更新。这样，这个缓存节点就会缓存旧的数据，造成缓存一致性的问题。

0x12 评估

这里的具体信息可以参看[2],

Small Cache, Big Effect: Provable Load Balancing for Randomly Partitioned Cluster Services

0x20 引言

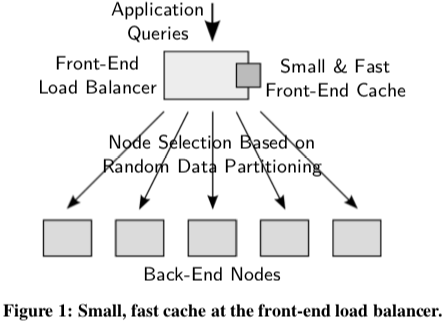
这篇Paper主要是证明了在一个类似下图的系统中，只需要缓存O(n*logn)级别的数据就能够很好地处理负载均衡的问题。这个结论是前面的好几篇Paper都引用了的，

we prove an O(n log n) lower-bound on the necessary cache size and show that this size depends only on the total number of back-end nodes n, not the number of items stored in the system. We validate our analysis through simulation and empirical results running a key-value storage system on an 85-node cluster.

0x21 证明

Paper假设的环境是一个支持基本的get、put接口的Key-Value的存储环境。另外它有这样的一些假设，

1. Randomized key mapping to nodes: each of m keys is assigned to one of the n storage nodes, and this mapping is unknown to clients.
2. Cache is fast enough: the front-end is fast enough to handle queries and never becomes the bottleneck of the system throughput.
3. Perfect Caching: queries for the c most popular items always hit the cache, while other items always miss the cache.
4. Uniform Cost: the cost to process a query at a back-end node is the same, regardless of the queried key or the back-end node processing the query.

• which m keys are stored on the system; 
• the number of back-end servers n; and 
• the cache size c.

假设系统中有m个keys，每一个访问的概率为p_i，这样就有 \(\\假设分布S = (p_1, p_2, ..., p_m), p_1 + p_2 + ...+ p_m = 1, 且假设 p_1 \geq p_2 \geq ... \geq p_m.\\ 如果缓存大小为c，则p_{c+1}之前的数据都在缓存中，其它的在后面的存储节点中。\\ 我们假设有 S: p_1 = p_2 =···= p_c = h≥ p_ c+1 ≥ ··· ≥ p_ m ≥0.\) 由于前面的c个的热点数据被Cache。要想在后面的存储节点中造成热点，最好的情况就是前面的c个Key的访问平均分配(因为这些反正被Cache了，访问偏斜反而会导致其它的Key访问频率降低)，且都不小于后面的Key。这样后面的访问频率会是一个“你消我涨”的情况，这里Paper中给出了具体的证明，示例如下图，

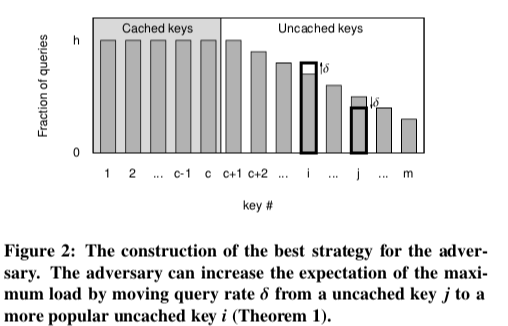
这样的最极端的情况所有的查询都是就是前面的x个Key(x <= m)，后面的Key都没有访问，也就是说 \(\\ S: p_1 = ... = p_c = h = p_{c+1} = ... = p_{x-1} \geq p_x \geq 0, p_{x+1} = ... = p_m = 0. \\ 即将查询平分给一些指定的Key，余下的一些查询分配给另外一个Key，即第x个。\) 根据将m个key平均随机分配到n给桶中的模型，每个桶中的Key的数量一个上限有， \(\\ \frac{M}{N} + \alpha\sqrt{2\cdot\frac{M}{N}\cdot\log N\ }. \\ 在这里没有被Cache的数据且有访问的数量为x-c给，设后面的服务器数量为n，则有:\\ \frac{x-c}{n} + \alpha\sqrt{2\cdot\frac{x-c}{n}\cdot\log n\ }. \\ 将所有查询R平均分配到x-1给key上面，则对于一个后端节点，最大的load的期望:\\ E[L_{max}] \leq (\frac{x-c}{n} + \alpha\sqrt{2\cdot\frac{x-c}{n}\cdot\log n\ } )\cdot\frac{R}{x-1}\\ 即 E[L_{max}] \leq (\frac{x-c}{x-1} + \alpha\sqrt{2\cdot\frac{x-c}{(x-1)^2}^\cdot n\log n\ } )\cdot\frac{R}{n}(稍微变换一下).\) 这里可以继续求E[L_max]的最坏的情况，即求极值，可以得到, \(\\E[L_{max}] \leq \frac{1+\sqrt{1 + 2\alpha^2\frac{n\log n}{c-1}}}{2}\cdot\frac{R}{n}, \\ 这里的重点是n\log n和c-1之间的关系，可以发现这里如果有c = k·n\log n + 1(k为常数)，则上面的式子有:\\ \frac{E[L_{max}]}{R/n} \leq \frac{1}{2}\cdot(1 + \sqrt{1+\frac{2\alpha^2}{k}\ }).\) 从而得到上面的结论。

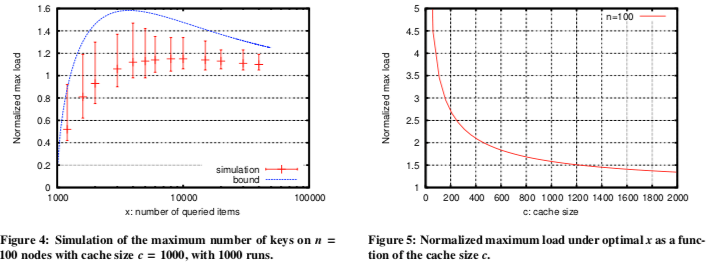
0x22 评估

这里的具体信息可以参看[3],

KeySched: Timeslot-based Hot Key Scheduling for Load Balancing in Key-Value Store

0x30 基本思路

KeySched是一片关于KVS负载均衡的一篇Poster。之前有几篇Paper是利用可编程交换机的来做相关的事情，而这里则是利用SmartNIC网卡来做，也就是说重点在于单机上面的Load Balancing。这里监控热点Key的方式是给予timeslot的方式，基本的方式在将时间分为一定程度的timeslot。使用Count-min Sketch之类的方式来发现热点key，然后将这个timeslot里面的热点的可以分配到最近的几个timeslots里面load最低的分区。基本的架构如下图，主要是三个基本组件。

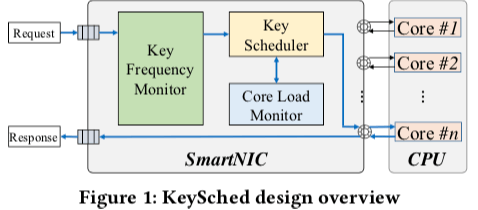
参考

1. Join-Idle-Queue: A novel load balancing algorithm for dynamically scalable web services. Perform. Eval. 68, 11 (2011).
2. DistCache: Provable Load Balancing for Large-Scale Storage Systems with Distributed Caching, FAST ‘19.
3. Small Cache, Big Effect: Provable Load Balancing for Randomly Partitioned Cluster Services, SoCC ‘11.
4. KeySched: Timeslot-based Hot Key Scheduling for Load Balancing in Key-Value Store, SIGCOMM ‘18.