Frequency-Counts/Quantile-Sketch over Data Stream

Approximate Frequency Counts over Data Streams

0x00 引言

这里总结的是这样的一类问题：给定两个用户指定的参数s和e，两者的取值范围都在(0,1)之间，且e远小于s。N表示一个流中目前经过的tuple的数量，这里的算法要满足/解决这个的几个条件/问题，1. 所有在itemset中的，出现频率高于sN被输出，且没有假阴性，也就是说达到了这个条件的必须被输出，2. 实际出现频率在(s-e)N之下的不会被输出，也就是说有假阳性，但是出现假阳性的item的频率会限制在一个范围之内，3. 估计的频率最大能够小于真实频率的值不能超过eN。注意这里并不需要计算实际的频率，只要超过一个阈值的即可，更加不需要实际出现的次数了。

0x01 Sticky Sampling Algorithm

Sticky Sampling算法中多了一个参数，这里用u表示。这里使用一个S集合，元素为(entry, f)，其中entry为元素，f为其出现频率的估计。算法中另外一个参数为r，表示采样率。在一个元素到达的时候，如果已经存在在S中，则对其f加1操作。否则，对到来的元素进行采样操作，采样率就是r。如果这个元素被选中，则添加到S中，f设置为1。初试的时候r 为 1，后面根据 $t = 1/e\log(s^{-1}u^{-1})$，开始的2t个元素设置r为1，接下来的2t个设置为2，在接下来的4t个设置为4，一次类推。Sticky Sampling算法最终选择其f不小于(s-e)N的元素进行输出。Sticky Sampling算法满足上面提到了3个条件。且最多会保存$2/e\log(s^{-1}u^{-1})$个元素

0x02 Lossy Counting Algorithm

Lossy Counting算法也是一个很简单的算法。基本思路是将流划分为窗口，这里使用w表示，w设置为1/e向上取整。算法维护一个数据结构D，保存的entry为(entry，f，delta)，前面两个的含义和前面的算法一致，delta表示最大可能的error。初始化的时候，D为空，在达到一个元素的时候，如果不存在D中，则添加一个(entry, 1, Bcurrent-1)，Bcurrent设置为N/w向上取整。如果已经存在D中，增加频率计数。在跨越窗口的时候，如果f + delta的值小于 Bcurrent，则删除。输出f不小于(s-e)N的元素。

0x03 其它一些

Misra-Gries(MG)算法也是一个很简单容易理解的算法。在数据处理中经常会用到，用于发掘出现频率最高的一些项。一个数据结构D，初始化为空。在一个元素到达的时候，如果已经存在D中。则将其计数值+1。如果不存在，且这个D中的原属数量小于预定义的最大值K，则将其计数值初始化为1加入D中。如果D中的元素数量已经达到了阈值K，则将其中的元素计数值-1，并移除其中计数值为0的情况。一些算法问题中长出现的一个问题就是如何在O(N)的时间内找出一个数组内出现次数超过一半的那个元素，其使用的算法可以看作为Misra-Gries(MG)算法的一种特殊情况。
Space Saving Algorithm，Space Saving算法也是一个很简答的算法。一个数据结构D，初始化为空，在一个元素达到是，会带有一个权重w。如果这个元素已经存在D中时，将其权重加上w，如果不存在其中，则将其权重加上D中最小权重元素的权重，并将这个最小权重的元素删除。

Space-Efficient Online Computation of Quantile Summaries

0x10 引言

和前面的从一个数据流中找出出现频率最高的一些元素不同，这篇Paper提出的算法是解决一个分位数统计的问题。这里可以将其称之为ϵ−approximate ϕ−quantile 分位数统计问题。即误差不超过ϵN的统计出第ϕ分位的数据，N为这个序列中元素的数量，ϕ为超过这个值占的比例，比如ϕ=0.5就是说超过50%的元素的值是什么。这里ϕ取值在[0，1]。这里提出的算法称之为GK Summary，用的比较广泛，在一些AI算法之中也使用了其和其的一些变体。

0x11 基本思路

算法的核心是维持一个数据结构S(n)，这个是一个排序的序列，其中的元素为(v-i，g-i，Delta-i)的结构，是一个目前已经见到的元素的子集。v-ib表示元素的值，这里， $S(n) = (v_0, g_0, \Delta_i),(v_1, g_1, \Delta_1),\cdots,(v_n, g_n, \Delta_n)，其中\\ g_i = r_{min}(v_i) - r_{min}(v_{i-1}), \Delta_i = r_{max}(v_i) - r_{min}(v_i), 另外\\ 特殊处理 i = 0时令g_0=1, i= s-1时，\Delta_{s-1}=0. 其中 \\ r_{min}和r_{max}方便代表值为v的时候最小和最大的rank。这样的话就有\\ r_{min}(v_i) = \sum_{j\le i}v_j, r_{max}(v_i)=\sum_{j\le i}g_j+ \Delta_i.$ 可以证明这里最大的误差为$max(g_i+\Delta_i)/2$。在GK Summary中查询，时查找第一个满足$r_{max}(v_j) > r + e$的j，返回$v_{j-1}$，如果找不到，则直接返回$v_{s-1}$。添加操作的时候，如果添加到最小 or 最大的边界，则直接添加(v, 1, 0)，如果添加到中间，则为$(v, 1, ⌊2ϵN⌋)$，这样就是使得添加这个元素的后面所有的元素的rank都增加了1，同时也满足了前面的g_i和Delta_i的条件。但是这样一直这样添加下面的话，S会变得很大。Delete操作就是将相邻的两个满足g_k之和小于等于2ϵN，$(v_{i+1}, g_i + g_{i+1}, \Delta_{i+1})$代替，连续满足条件的一致替代，这样就减小了S。这里没有改变$\Delta_{i+1}$。另外GK Summary还要Compress操作。这里引入了Band的概念， $定义 p=⌊2ϵN⌋，给定\Delta，定义一个summary的capactity=p−Δ，则band=⌊log2(capactity)⌋。$ 这里具体的思想可以参看论文[1], Compress的伪代码如下。算法从s-2到0扫描entries，满足Band条件之后进行删除的操作。这里的思路，根据上面的定义，是选择band更大的，capacity就越大。这样选择留下band更大能带来更大的capacity。

这里的Compress操作在满足一定的条件下才会触发，论文中设置的是n每次增加1/2e的时候执行一次compress操作，GK Summary的空间复杂度为$O(1/e\log(eN))$，平摊的时间复杂度为$O(\log(1/e)+\log\log(eN)$，证明略，具体可以参看[1,5]。Paper[5]中提到了GK算法的几个变体。

GKAdaptive，GKAdaptive在中间添加的时候，添加$(v, 1, g_i + \Delta_{i-1}-1)$，而不是(v, 1, ⌊2ϵN⌋)。在接下来添加的时候，尝试移除一个可以移除的元组。这里的一个问题是如何发现这个可以移除的元组，[5]中提出的方法是维护一个使用$g_i+g_{i+1}+\Delta_{i+1}$的最小堆来实现。在添加一个元素的时候，先检查这个添加的添加的元素是否可以移除，可以的话直接移除。否则检查堆顶元组，可以移除的情况下移除这个元组。[5]这里的实现不会调用Compress操作。

GKMixed， GKMixed变体看上去就是其结合体。GKMixed也会调用Compress操作，

In this variant, called GKMixed, after inserting an element, we first check if it is removable. If so, we remove it right away. Then, whenever |L| doubles, we call COMPRESS to remove tuples. For this variant, the O(1/2 * log(εn)) space bound still holds.

A Fast Algorithm for Approximate Quantiles in High Speed Data Streams

0x20 基本思路

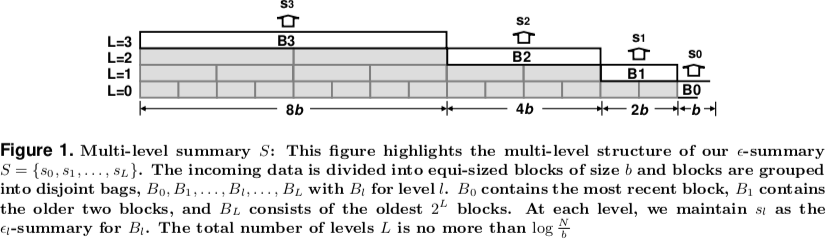
这里的算法的基本思路如上图所示。这里是一个多层的结构，算法更新的伪代码如下图。这里的一个重要参数是b，这里$b=⌊\log(eN)/e⌋$，在s0，即第0层的summary没有满的时候，直接统计，操作结束。如果满了，则执行排序、Compress操作，将s0置为空。接下来的循环的操作就是看能不能将前面的sc设置为这一层 or 合并压缩。压缩操作回增加误差，将summary里面的元素数量减半，准确地说是b/2向上取整再加1。

Paper中将这个算法拓展到流时的环境中，使用的是将其分区/分段的方法。前面的两个算法都要求N是已知，而这里不需要。基本思路是将流划分为$P_i = [(2^i-1)/e,(2^{i+1}-1)/e)$的段，每段的长度为2^i/2，可以发现这里段的长度是加倍增加的。最终回答rank的时候，使用下面伪代码的第二个参数回答。

参考

Approximate Frequency Counts over Data Streams, VLDB ‘02.
A High-Performance Algorithm for Identifying Frequent Items in Data Streams, IMC ‘17.
http://sites.nlsde.buaa.edu.cn/~yxtong/bd2016/07_Streaming_1027.pdf
Space-Efficient Online Computation of Quantile Summaries, SIGMOD ‘01.
Quantiles over Data Streams: An Experimental Study, SIGMOD ‘13.
Moment-Based Quantile Sketches for Efficient High Cardinality Aggregation Queries, VLDB ‘18.