Cold Filter: A Meta-Framework for Faster and More Accurate Stream Processing

0x00 引言

这里一次性看了PKU的几篇类似的Paper，不得不佩服其发paper的效率。而且这些Paper和前面的几篇在SIGCOMM中方便的几篇讲Sketch用在网络策略中的存在一些联系。Cold Filter就是一种Sketch的设计，利用一种Sketch来做Filter。与一般的Count Sketch和Count-min Sketch的设计不同。Cold Filter这里主要的idea就是引入一个两层的设计。Coun Sketch这样的存在几个缺点，一个就是内存效率不高，为了能计数到比较大的值，这里就要使用更多的bit来作为一个计数的单位。但是实际的数据大部分出现的次数都是比较小的，而且访问不均衡的现象很常见。这个就是引入两层计数方式的基本出发点，

... Our filter can accurately estimate both cold and hot items, giving it a genericity that makes it applicable to many stream processing tasks. To illustrate the benefits of our filter, we deploy it on three typical stream processing tasks and experimental results show speed improvements of up to 4.7 times, and accuracy improvements of up to 51 times.

0x01 基本思路

CF的基本思路就是一个两层的设计，其中L1记录大部分数据访问统计，这部分使用一个较少的bit作为计数的单元。而未来处理一些热点的数据，在计数值超过了L1能够计数的范围之后，将其计数到L2中。在CF中，一个更新操作的处理流程如下，

• 使用hash函数产生多个hash值，利用这些hash值在L1中找到对应的位置，如果其中的最小值小于L1计数的范围。那么这个时候直接更新最小值。如果存在多个最小值，则更新全部的最小值。如果L1已经超出了计数的范围，则在L2执行同样的的操作。

同理，在执行report操作的时候，也要考L1和L2的情况，

• 使用hash函数产生多个hash值，利用这些hash值在L1中找到对应的位置，如果其中的最小值小于L1计数的范围，则报告这个值。如果超过了L1的计数范围，则以同样的方式查找L2，如果L2的计数没有超过，则报告L1和L2的和。如果两个地方都超出了，则很难判断这里的具体情况，这里就直接选择超出了指定的阈值。

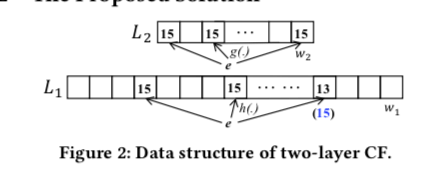
在基本的算法只是，CF还利用其它的一些优化方式。这里的思路其实在其他的算法中也用到过，这里如果将L1的bit数置为1的话，就类似于一个Bloom Filter结构，在经过这个Bloom Filter过滤之后在在L2中的Sketch中计数，从而节省空间，这个思路被用到了TinyLFU中。实现在Java的本地缓存库Caffeine中。

0x02 评估

这里具体信息可以参看[1].

HeavyGuardian: Separate and Guard Hot Items in Data Streams

0x10 引言

HeavyGuardian实际上的核心也就是是Frequency Estimate。同样地，这里也主要是优化少数的热点数据和大量的较冷的数据计数的问题。与前面的Cold Filter的使用两层的思路有类似的地方，HeavyGuardian也是利用较冷数据和热点数据分开计数的思路，不过在具体的实现方式方面存在明显的差别。

0x11 基本思路

HeavyGuardian的基本思路如下。HeavyGuardian的基本数据结构是一个Hash Table。对于这个Hash Table的每一个Bucket分为了两个部分，一个是Light Part，用来计数冷数据的访问统计，另外一个是Heavy Part，用来计数热点数据的访问统计。Heavy Part的部分，里面包含多个Key-Value的Pair，其中的Key为ID，Value为计数器count。Light部分则直接使用类似二层数组的方式，

... We use A[i][j]h (1 ⩽ i ⩽ w,1 ⩽ j ⩽ λh) to denote the jth cell in the heavy part of the ith bucket, and use A[i][j]h.ID and A[i][j]h.C to denote the ID field and the count field in the cell A[i][j]h, respectively. Among all KV pairs within the heavy part of one bucket, we call the hottest item (i.e., the item with the largest frequency) the king, call other items guardians, and call the guardian with the smallest frequency the weakest guardian.

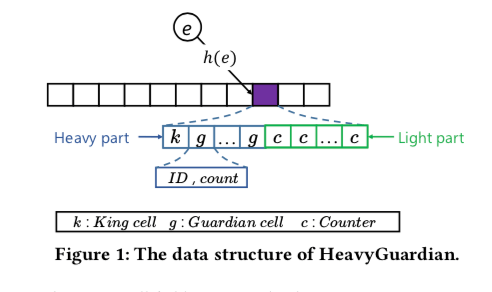
在HeavyGuardian中的操作如下，

• 添加操作，多余要添加的记录e，首先计算其hash值，找到对应的bucket。这里会先尝试添加到Heavy Part，没有的情况下添加到Light Part。1. 如果这里时候在Heavy Part存在这Key的记录，直接递增对应的count即可； 2. 如果没有，则找到一个空闲的cell，设置其ID为e的Key，count值为1；3. 如何在Heavy Part中没有记录，也没有空闲的cell的时候。这里引入了Exponential Decay的策略。这里以一定的概率对weakest guardian进行减1操作，这个概率为p = b^-C，这里的b为预定义的，Paper中选择了1.08，C为weakest guardian的计数器。在递减操作，如果weakest guardian变为0，则设置其ID为e的key，count值为1。如果不为0，则添加到light part中。
• 在添加到light part的时候，使用另外一个hash函数的时候，对A[h(e)][h′(e)]进行加1操作。在查询操作的时候，首先查询Heavy Part的部分。如果没有发现，在利用添加到light part的部分的方式查询light part部分。

0x12 评估

​ 这里具体信息可以参看[2].

HeavyKeeper: An Accurate Algorithm for Finding Top-k Elephant Flows

0x20 引言

HeavyKeeper这里是利用Stekch来统计在TCP flow大小Top-k信息的一种方法。HeavyKeeper利用近似的频率统计加上其它的一些策略和优化方式，实现Top-k的统计，

... In this paper, we adopt a new strategy, called count-with-exponential-decay, to achieve space-accuracy balance by actively removing small flows through decaying, while minimizing the impact on large flows, so as to achieve high precision in finding top-k elephant flows.

0x21 基本思路

在统计频率上面，这里使用的带Footprint的Count-min Sketch的思路。在d个数组中的每个元素都有两个部分组成，一个footprint和一个计数字段C。在这里执行添加操作方式如下，

• 初始化的时候，所有的footprint字段均为null。对于每一个流fi的包，计算出d个hash值。这里有三种情况。1. 对于一个hash值对应的位置的C为0，则将footprint设置为这个流fi的footprint，C设置为1；2. 如果C不为0，且footprint也对应上流，则将计数字段C递增；3. 如果footprint字段对应不上，则使用前面类似的exponential-weakening decay策略，以一个概率值Pdecay递减这个计数字段。如何递减之后计数字段为0，则重新设置footprint为这个fi的，设置C为1。这里的Pdecya的思路和前面的HeavyGuardian一样，Pdecay = b ^ -C，这里的b为预定义的，Paper中选择了1.08，C为的计数器值。
• 查询操作的时候，它计算出来d个函数值，根据对应的位置，选择其中footprint对应上中计数值C最大的。

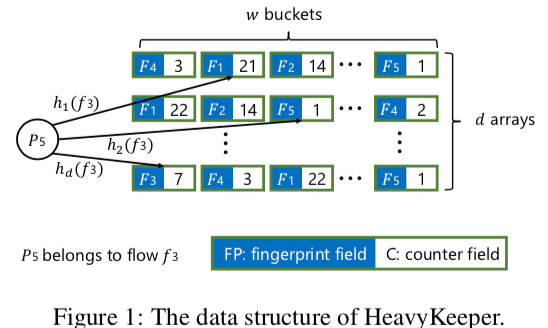
在这个基础还是不够。实现Top-k查询基本思路是在这里引入一个mini-heap。基本操作思路如下，对于一个流fi，根据前面的数据结构获取到统计数据n。如何fi已经在这个min-headp中了。则设置为max(n, min heap[fi])，即保存在计数数据结构和min heap中的较大值。另外，如果这个n大于其中的最小值，则最小的删除，添加这个新的fi的数据进去。在此的基础之上，这里还引入了几种优化策略，

• Finger print Collisions Detection，在有fingerprint冲突的时候，会造成计数器C偏大。这里缓解的策略是如果一个流fi不存在在min heap中，但是计数值n却大于n-min+1，即min heap最小值，不对这个fi进行添加到min heap中的操作。
• Selective Increment，同样地基于上个优化的思路，发现大于n-min + 1的时候，不进行递增计数 or 递减的操作。

0x22 评估

这里的具体信息可以参看[3].

Pyramid Sketch: a Sketch Framework for Frequency Estimation of Data Streams

0x30 引言

这里是引入了一个类似金字塔的结构，在其他的Sketch算法上面实现一个新的Sketch算法。所以这里称之为Pyramid Sketch，而且是一个Framework。它的思路也是很有意思，

we applied our framework to four typical sketches. Extensive experimental results show that the accuracy is improved up to 3.50 times, while the speed is improved up to 2.10 times.

0x31 基本思路

这里的思路感觉和Path Hashing的思路存在类似的地方。在这里下一层的计数overflow的时候，向上一层进行carryin操作。处理最底层的Sketch之外，上层的Sketch的每个entry都包含了三个部分，left flag、right flag和一个计数的部分。

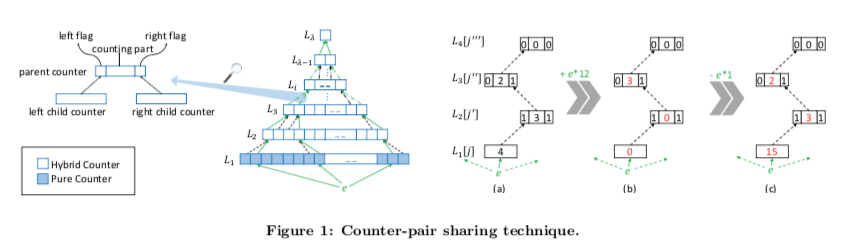
在Pyramid Sketch中一些操作如下，

• 计算出元素的d个hash值，根据这些hash值寻找第一层的计数器。这里在不同的层使用不同的增加策略。除了第一层外，其它的层计数器有δ−2个bit。
• 如果一层的计数overflow了，则查找其上面的parent counter。这里假设为上一层的左子节点。这个时候如果其lflag没有设置，则将其设置，并递增其counter part。如果设置了，直接递增counter part即可。同样地，如果这一层overflow了。则在向上面carryin操作美酒相当于将一个bit数量较大的计数器分割为好几个部分，通过将高位bit的合并减少占用的空间数据。。
• 在Pyramid SKetch中执行删除操作只有在使用的基本的Sketch算法为可以支持删除操作的情况下它才可以执行删除操作。删除操作实际上是递减的操作，执行的操作过程和添加的操作即递增的操作相反。这里在一层不为0的时候对其进行递减，在为0的时候，设置为2^(δ−2)−1。

根据前面的基本算法，在Pyramid SKetch查询操作如下图。这里是一个递归的操作，最终的结果也是个层计数的和。不过这里要注意不同层计数的差别，而且在lflag和rflag均为true的情况下计数的策略。在两个flag都设置的情况下，这里表面另外一方的也至少对其进行了一次的递增操作，这里就想将计数器减1之后在乘以系数。在非底层的报告数量的时候，注意要乘以这层的系数。这个的系数。如歌将每层的计数组合为一整个整数的，就可以得知这个系统的来源了。

在基本策略上面，Pyramid Sketch还引入了其它的一些优化策略。

0x32 评估

这里的具体信息可以参看[4].

参考

1. Cold Filter: A Meta-Framework for Faster and More Accurate Stream Processing, SIGMOD ‘18.
2. HeavyGuardian: Separate and Guard Hot Items in Data Streams. SIGKDD ‘18.
3. HeavyKeeper: An Accurate Algorithm for Finding Top-k Elephant Flows. ATC ‘18.
4. Pyramid Sketch: a Sketch Framework for Frequency Estimation of Data Streams. VLDB ‘17.