Wormhole: A Fast Ordered Index for In-memory Data Management
0x00 引言
这篇Paper提出的思路很新颖。它用一种新思路设计了一种支持范围查找数据结构。Wormhole可以支持最坏在O(logL)的时间复杂度下面查找一个Key。一般的平衡树or Skiplist结构点查询的复杂度都是O(logN),这里N是Key的数量,基于trie的数据结构的复杂度一般为O(L),这里的L为Key的长度,而Wormhole点查询的复杂度是O(logL),而且其它方面的表现也很不错,
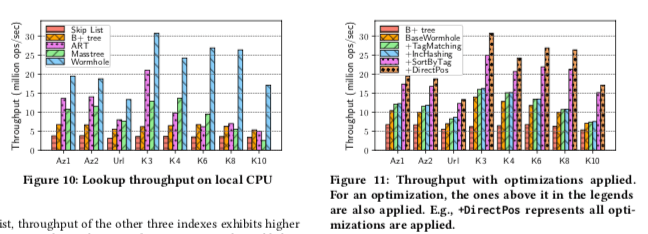
... Wormhole’s index space is comparable to those of B+ tree and skip list. Experiment results show that Wormhole outperforms skip list, B+ tree, ART, and Masstree by up to 8.4×, 4.9×, 4.3×, and 6.6× in terms of key lookup throughput, respectively.
0x01 MetaTrie
B tree的数据结构一般都很熟悉,它是一个节点的子节点数很多的数据结构。由于分叉的数目很大,B tree的数据绝大部分都是保存在叶子节点上面的。而B+ tree只会将数据存放在叶子节点上面,结构比B tree简单一些。在这篇Paper中,将B+ tree的内部的节点部分称之为MetaTree,叶子节点组成的list称之为leaf list。
-
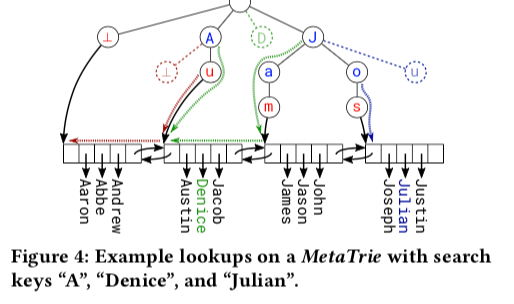
Paper的第一个对B+ tree的改动就是将B+ tree的MetaTree改为Hash Table,这样的话点查询的理论复杂度就是O(1),结构如下图所示。很显然,在查询的时候,这样的数据结构是可以支持范围查找的,但是无法支持添加操作的时候将数据添加到正确的位置。支持顺序添加操作可以通过使用Tire的方式实现,这里的一个改动是使用Trie来替代Hash Table。这里使用MetaTire代替B+ tree的MetaTree。在这样的设计中,查询和添加的复杂度都是O(L)。在MetaTrie中,查找的操作分为两步,第一步是查找search key和anchor key的最长前缀匹配,在匹配的情况下,就在leaf node中查找。如果不匹配,则需要在leaf node中查找,如下图中红色线和绿色线表示的一样。
0x02 Wormhole
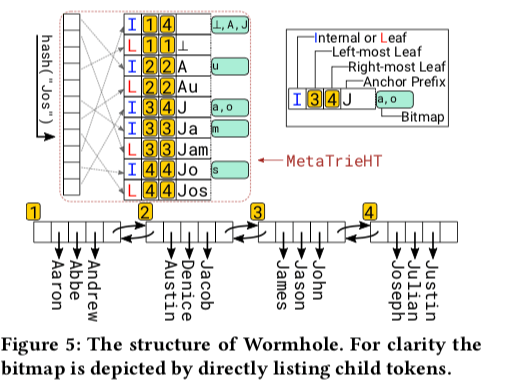
使用Tire只能达到O(L)的复杂度,为了达到O(Log(L))的复杂度,这里使用了基于一种Hash Table的优化方式。这种方式在来自于一种IP路由查找算法。基本思路如下:1. 使用binary search on prefix lengths来查找最长前缀匹配,这个方法就是一种网络中加速routing table查找的算法。将一个anchor key的所有的前缀都加入到作为索引的Hash Table中。例如“Jam” 作为一个anchor key,则其前缀(“”, “J”, “Ja”, “Jam”)都加入到Hash Table中。在查找的时候,使用二分查找的方式查找最长匹配前缀。2. Hash Table的基本设计如下图,这个Hash Table称之为MetaTrieHT。用于替代前面的MetaTrie中的Tire。每个Entry使用,使用一个字段表示这个节点是一个achor or 一个leaf node。另外的两个标记字段标记是否是最左or最右的leaf node。实际上Hash Table为Leaf List上面的索引结构。bitmap用于加速第二阶段的查找,
The bit is set when the corresponding child exists. With the bitmap, sibling(s) of an unmatched token can be located in O(1) time. Trie node corresponding to a hash item can be considered as root of a subtree.
在Wormhole中查找的基本算法如下伪代码,其核心就是在TireHT中的查找操作。将一个Key的所有的前缀都加入到Hash Table中一般会被认为空间效率不高。但是这里确认为Wormhole空间效率很不错,主要是因为这里interna node的空间很大程度上取决于key的内容。在Key比较不分散有较长的前缀的时候,这样很多Key会共享一些数据,节约了内存。另一方面,如果Key很分散,没有多少共同的前缀,则这里需要处理的anchor key的长度也会比较小,这里保存的数据也不会非常多。这里如何在实现的时候选择一个合适的anchor key是一个比较核心的问题。
function GET(wh, key)
leaf ← searchTrieHT(wh, key);
i ← pointSearchLeaf(leaf,key);
if (i < leaf.size) and (key = leaf.hashArray[i].key) then
return leaf.hashArray[i]
else
return NULL
function searchTrieHT(wh, key)
node ← searchLPM(wh.ht, key, min(key.len, wh.maxLen))
if node.type = LEAF then return node
else if node.key.len = key.len then
leaf ← node.leftmost
if key < leaf.anchor then leaf ← leaf.left
return leaf
missing ← key.tokens[node.key.len]
sibling ← findOneSibling(node.bitmap, missing)
child ← htGet(wh.ht, concat(node.key, sibling))
if child.type = LEAF then
if sibling > missing then
child ← child.left
return child
else
if sibling > missing then
return child.leftmost.left
else
return child.rightmost
其它的一些基本操作的伪代码如下,
functionSET(wh,key,value)
leaf ← searchTrieHT(wh, key);
i ← pointSearchLeaf(leaf,key);
if (i < leaf.size) and (key = leaf.hashArray[i].key) then
leaf.hashArray[i].value ← value
else
if leaf.size = MaxLeafSize then
left, right ← split(wh, leaf)
if key < right.anchor then
leaf ← left
else leaf ← right
leafInsert(leaf, key, value)
functionDEL(wh,key)
leaf ← searchTrieHT(wh, key);
i ← pointSearchLeaf(leaf,key);
if (i < leaf.size) and (key = leaf.hashArray[i].key) then
leafDelete(leaf, i)
if (leaf.size + leaf.left.size) < MergeSize then
merge(wh, leaf.left, leaf)
else if (leaf.size + leaf.right.size) < MergeSize then
merge(wh, leaf, leaf.right)
function RangeSearchAscending(wh,key,count)
leaf ← searchTrieHT(wh, key);
incSort(leaf.keyArray);
out ← []
i ← binarySearchGreaterEqual(leaf.keyArray, key)
while (count > 0) and (leaf != NULL) do
nr ← min(leaf.size - i, count);
count ← count - nr
out.append(leaf.keyArray[i : (i + nr - 1)])
leaf ← leaf.right;
i ← 0
if leaf != NULL then incSort(leaf.keyArray);
return out
function pointSearchLeaf(leaf, key)
i ← key.hash × leaf.size / (MAXHASH + 1);
array ← leaf.hashArray
while (i > 0) and (key.hash ≤ array[i - 1].hash) do i ← i - 1
while (i < leaf.size) and (key.hash > array[i].hash) do i ← i + 1
while (i < leaf.size) and (key.hash = array[i].hash) do
if key = leaf.array[i].key then return i
i←i+1
return i
function allocInternalNode(initBitID,leftmost,rightmost,key)
node ← malloc(); node.type ← INTERNAL
node.leftmost ← leftmost; node.rightmost ← rightmost
node.key ← key; node.bitmap[initBitID] ← 1
return node
functionincSort(array)
if array.sorted.size < THRESHOLD then array ← qsort(array)
else array ← twoWayMerge(array.sorted, qsort(array.unsorted))
同样地,B-tree中节点合并和分裂的操作在这里也会是一个比较麻烦的操作,
function split(wh, leaf)
incSort(leaf.keyArray); i ← leaf.size / 2
while Cannot split between [i−1] and [i] in leaf.keyArray do
Try another i in range [1, leaf.size −1]
Abort the split if none can satisfy the criterion
alen ← commonPrefixSize(leaf.keyArray[i−1], leaf.keyArray[i])+1
newL ← malloc(); newL.anchor ← leaf.keyArray[i].key.prefix(alen)
key ← newL.anchor; Append 0s to key when necessary
wh.maxLen ← max(wh.maxLen, key.len)
Move items at [i to leaf.size−1] of leaf.keyArray to newL
Insert newL at the right of leaf on the leaf list
htSet(wh.ht, key, newL)
for plen : 0 to key.len−1 do
prf ← key.prefix(plen); node ← htGet(wh.ht, prf)
if node.type = LEAF then
parent ← allocInternalNode(0, node, node, prf)
htSet(wh.ht, prf, parent); prf.append(0);
node.key ← prf htSet(wh.ht, prf, node); node ← parent
if node = NULL then
node ← allocInternalNode(key[plen], newL, newL, prf); htSet(wh.ht, prf, node)
else
if node.leftmost = leaf.right then node.leftmost ← leaf
if node.rightmost = leaf.left then node.rightmost ← leaf
function merge(wh,left,victim)
Move all items from victim to the left node
key ← victim.key; htRemove(wh.ht, key)
for plen : key.len−1 to 0 do
prefix ← key.prefix(plen); node ← htGet(wh.ht, prefix)
node.bitmap[key[plen]] ← 0
if node.bitmap.isEmpty() then htRemove(wh.ht, prefix)
else
if node.leftmost = victim then node.leftmost ← victim.right
if node.rightmost = victim then node.rightmost ← victim.left
并发
Wormhole中,三种不同类似的操作需要不同类似的锁。第一种类型的是点查询和范围查询,不会修改数据,也不要求独占访问数据。第二种类型是添加 和 删除操作,涉及到一个 or 多个 leaf node修改。第三种是会设计到节点合并和分裂操作的添加和删除操作。为了提高Wormhole操作的并发性,这里使用了两种不同类似的Lock,第一种是RWLock,用在每个Leaf Node上面,被用于第一二中类型的操作。对于第三种类型的操作,会设计到多个Hash Table中Entry的修改和多个Leaf Node修改,这里直接就使用Mutex,对整个的TireHT加锁。这样带来的问题就并发性不高。为例解决这个问题,这里引入了QSBR RCU机制,reader可以lock-tree地访问TireHT。这样只会Writer会使用这个Mutex,
To perform a split/merge operation, a writer first acquires the lock. It then applies the changes to a second hash table (T2), an identical copy of the current MetaTrieHT (T1). Meanwhile, T1 is still accessed by readers.
查找操作在达到leaf node的时候,这里需要保存这个操作过程中Hash Table和Leaf List保持一致。对于第三种类型的添加 or 删除操作,先对对应的leaf node加锁,如果设计到多个leaf node,从左到右加锁。然后在MetaTrieHT加mutex lock,这个时候就可以进行实际的操作。为了减少对reader的影响,这里会每个结构更新操作完成之后就会解锁,为了保持一致性,这里使用了一个version number的方式。
0x03 评估
这里的具体信息可以参看[1], 从Paper中的测试数据来看,Workhoke各个方面的性能都不错。
参考
- Wormhole: A Fast Ordered Index for In-memory Data Management,EuroSys ’19,
