DianNao: A Small-Footprint Accelerator for Large-Scale Neural Networks
0x00 引言
这篇Paper是著名的“电脑”系列论文的第一篇。常见的Neural Networks如CNN、DNN之类中,体现在CPU上面的运算的话,绝大部分的运算都是矩阵/向量彼此之间的运算,比如矩阵乘法,矩阵-向量相乘等等。一般高性能计算入门的就是一个矩阵乘法的运行,简单的串行版本在优化之后甚至可以获得上万倍的性能提升。虽然CPU目前有SIMD指令的加持,不过用CPU去计算这样类型的计算还是不是非常适合。这样就给了这样的Domain Specific的结构设计机会,
We show that it is possible to design an accelerator with a high throughput, capable of performing 452 GOP/s (key NN operations such as synaptic weight multiplications and neurons outputs additions) in a small footprint of 3.02mm^2 and 485mW; compared to a 128-bit 2GHz SIMD processor, the accelerator is 117.87× faster, and it can reduce the total energy by 21.08×.
0x01 运算特点
CNN、DNN之类的网络基本的组成是一组的layers/层,常见的比如卷积层/convolutional layers、池化层/pooling layers,和分类层?/classifier layers等。卷积为多次的矩阵乘法,池化为一个矩阵上面的一种运算,而classifier layers很多是矩阵-向量乘法。比如下面的这个例子,

第一个版本的事没有任何优化的朴素实现。下面的这个优化主要是访问局部性的优化。基本的思路就是将参与其中的矩阵-向量发片,常见的分片大小根据CPU的Cache Line大小,Cache大小,以及SIMD宽带等的因素决定。这个在很多的高性能计算中是常见的优化思路。在朴素版本的实现中,内存上面的数据传输量主要来自于input loaded + synapses loaded + outputs written 三个部分。Ni × Nn + Ni × Nn + Nn。通过下面tiling的优化方式,在Paper中测试的一个CLASS1 case中,内存的使用的带宽有原来的120GB/s可以下降到大约几个GB/s。

卷积层和持久化层这样的局部性优化思路是一样的,不过具体的复杂程度高了很多。卷积层这里会有多个卷积和,卷积核以滑动窗口的方式可以输入矩阵的部分依次相乘,不同卷积核求得的结构在求和。这个是很多个的循环,在进行了tiling的优化之后,这个循环就更加复杂了。这个如果先给出一个矩阵乘法的这样的优化思路,然后给出一份矩阵乘法的这样的优化代码,在拓展到这个卷积计算可能看上去会更加清晰一些,

池化层在没有优化之前的代码就是矩阵上面的字矩阵的运算,也是类似滑动窗口的方式。这里的例子是最大池化和平均池化的例子。不过优化之后的优点复杂了,¯_(ツ)_/¯

0x02 基本设计
上面的的卷积、池化以及分类代码的优化就是DianNao加速器设计的思路。其想法是,和CPU相比,尽可能地一次性计算更加多的运行。这些基本的矩阵-矩阵,矩阵-向量,向量-向量运行模式比较固定,优化起来相对来说要简单一些。下图就是DianNao加速器的基本设计,有这样的基本组件:1. NBin,NBout分别为输入、输出神经元的缓冲区,2. 保存突触权重的缓冲区SB、synaptic weights,3. 计算部分Neural Functional Unit (NFU),4. 控制逻辑部分Neural Functional Unit (NFU)。
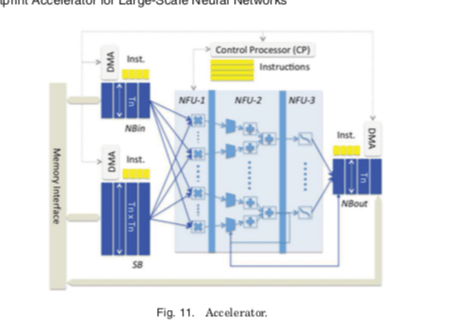
NFU部分主要是三个子部分。不同的操作被分为2-3个阶段完成。比如对于分类层来说,就是矩阵乘法 加上 最后的乘法以及sigmoid函数的计算。卷积层的运算和分类层的运算时类似的。池化层不同的是会有多个结果值求和的运行,所以还要用到加法。NFU的NFU-1部分是16x16的乘法器,这256个乘法器可以同时运算。NFU-2是加法树的结构。NFU-2主要对用到池化的一些操作,所以这里会包含shifters和max之类的操作。第三层主要对应到网络中的激活操作,比如使用sigmoid函数。这里sigmoid可以可以使用一个piecewise linear interpolation 的方式实现( f (x) = ai × x + bi,x ∈ [xi;xi+1]),而且只会损失很少的精度。这样在硬件上面就是实际对应到两个16 × 1 16-bit multiplexers,一个16-bit multiplier和一个16-bit adder 。16-segment的两个系数(ai , bi)保存在一个小的RAM中。通过改变这些系数,这里不仅仅可以实现sigmoid函数。其它的函数也同样方便实现,比如hyperbolic tangent, linear functions等。计算使用16bit的顶点数,实际上不会比32bit的浮点数损失很多的精度,但是可以大大减少计算量。
- 运算的时候,网络的参数先加载到SB中,输入数据加载到NBin中。经过NFU的运算之后的结果输出到NBout中。具体的矩阵-矩阵,矩阵-向量,向量-向量运算会使用前面分片/tiling的思路转化为这里的运算。方便一次性并行计算多个,而且这个的三个阶段经过NFU一次性运算完成。
- Paper中另外也提到了一些芯片实现上的细节。比如SB,NBin和NBout的分离设计。这部分访问的带宽等特性存储明显的差异,这样分离设计更加好。另外的就是一些局部性上面的优化,比如数据的计算和加载进行流水线处理等。
0x03 评估
这里的具体信息可以参看[1].
DaDianNao: A Machine-Learning Supercomputer
0x10 基本架构
DaDianNao的电脑和DianNao论文发表在同一年。DaDianNao可以看作是在DianNao上面的一些规模上的拓展思路。这里出发是使用多片系统/multi-chip system来实现更高的性能。在DianNao中,主要瓶颈是内存带宽,主要在卷积层和分类层,而且SB/NBin/NBout要求的带宽存在较大的差别,
For these types of layers, the total number of required synapses can be massive, in the millions of parameters, or even tens or hundreds thereof. For an NFU processing 16 inputs of 16 output neurons (i.e., 256 synapses) per cycle, at 0.98GHz a peak bandwidth of 467.30 GB/s would be necessary.
内存带宽作为主要的瓶颈给DaDianNao设计的影响就是, 将参数(也就是SB保存的数据)放在靠近使用其的NFU的地方,减少访问延迟和数据移动。而且这里不要有主存参与,为一种分布式的结构。 一种根据存储而非计算的非对称结构。还有其它的一些内存带宽的优化等。下图是其中一些结构的基本设计。DaDianNao是一种分片式的设计,在下图中式有16个分片,每个分片内部的结构如图5右所示。中间是NFU,和前面的DianNao的NFU是同一个东西,不同的地方在于其周围的存储介质。在DaDianNao中,SB的数据就保存在这些eDRAM中。而在DianNao中,使用的SDRAM保存。DaDianNao认为虽然eDRAM比起SDRAM性能差一些,但是有更高的存储密度,更低的功耗。而eDRAM也需要和DRAM一样,要定期刷新来保证数据不丢失,这里将eDRAM分为4块,可以可以降低周期性的刷新操作的影响,而且可以使得其位置于NFU更加靠近。又通过分片的设计降低了不同计算部分的相互影响。
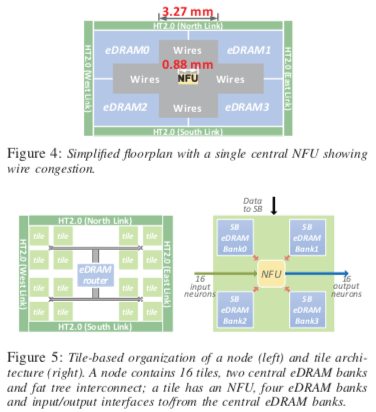
DaDianNao Paper中给出了下面的一些eDRAM和NFU流水线操作的例子。上面的DianNao的论文中只是文件描述,这里表示地更加清晰一些。总结下来就是DaDianNao中NBin和NBout保存在中心的一个eDRAM中,而SB发布在16个eDRAM中。这样可以看出来DaDianNao和DianNao两个差异看出DaDianNao改变的思路:分片设计,使用多个NFU,每个NFU使用自己的保存SB的eDRAM;根据带宽要求的不同分别保存不同的数据等。
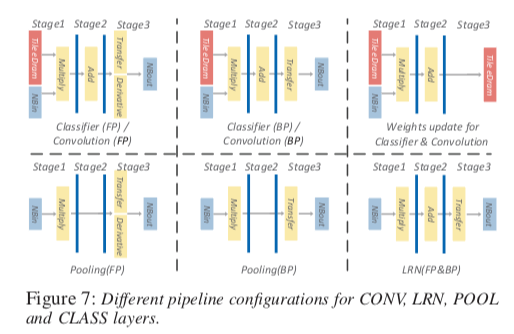
另外,在DaDianNao基本的设计上面,还提出了通过HyperTransport (HT)来多片互联的架构。
0x11 评估
这里的具体内容可以参看[2].
PuDianNao: A Polyvalent Machine Learning Accelerator
0x20 引言
DianNao系列论文中的这篇的核心是给出一种通用的机器学习加速器的设计,讲到了常见的一些算法的加速设计:k均值、k临近、朴素贝叶斯、SVM、线性回归、分类树和DNN等七种,
PuDianNao can perform up to 1056 GOP/s (e.g., additions and multiplica- tions) in an area of 3.51 mm2, and consumes 596 mW only. Compared with the NVIDIA K20M GPU (28nm process), PuDianNao (65nm process) is 1.20x faster, and can reduce the energy by 128.41x.
0x21 算法
Paper中先分析了从体系结构的角度来优化的机器学习算法的思路,
-
k临近算法的一个朴素的计算举例的方式就是一个二层循环,在使用分片的优化之后,内存带宽的需求下降了93.9%,
//Na is the number of testing instances //Nb is the number of reference instances for (i = 0; i < Na; i++) { for (j = 0; j < Nb; j ++) { Dis[i,j] = dis(t(i),r(j)); }} //Ti is the tiled testing block size //Tj is the tiled reference block size for (i = 0; i < Na/Ti; i++){ for (j = 0; j < Nb/Tj; j ++){ // tiled block for (ii = i*Ti; ii < (i+1)*Ti; ii++) { for (jj = j*Tj; jj < (j+1)*Tj; jj++) { Dis[ii,jj] = dis(t(ii),r(jj)); }}}} -
k-Means中也多的也是点之间距离的计算。算法从几个随机的点出发,迭代计算根据距离调整质心的距离。同样的优化思路可以降低89.83%的内存带宽需求。
-
Deep Neural Network算法中,以前馈计算/feedforward computation为例。计算被抽象为计算这样一个式子, \(y_j =f(\sum_{i=1}^{N_a}w_{ij}x_i+s_j).\\\) 基本的代码和优化之后的代码如下。测试发现下面优化的方式可以节省46.7%的内存带宽。不过这里的代码if(j == Na)这个分支明明可以移到循环之外单独处理,这样更容易用SIMD处理,接受判断指令。
//x is the input neurons, y is output neurous //w is the weights, w[0,i] = s[i] y(all) = 0; //initialize all neurons for(i = 0; i < Nb; i++){ for(j = 0; j < (Na+1); j ++){ y[i] += w[j,i]*x[j]; if(j == Na) y[i] = f(y[i]); }} //T is the tiled block size y(all) = 0; //initialize all output neurons for (j = 0; j < (Na+1)/T; j ++) { // tiled block for (i = 0; i < Nb; i++) { for (jj = j*T; jj < T; jj ++) { y[i] += w[jj,i]*x[jj]; if(jj == Na) y[i] = f(y[i]); }}} -
线性回归,在训练阶段可以抽象为一个Y = θX式子的计算,实际上就是一个矩阵-向量的乘法。这样实际上计算的时候计算模式和前面的算法没有很大的差别。
-
SVM、朴素贝叶斯和分类树等,也都可以抽象为矩阵-向量之间的一些计算。
0x22 基本思路
PuDianNao的主要思路是在DianNao的思路上面添加可以可以支持更加通用计算的单元,以达到可以实现更多算法的目的。其主要的结构是多个的FU/功能单元,每个功能单元是一个MLU和ALU的结合。三个数据缓存组件,分别用于输出、热数据和冷数据。另外还有一个指令缓存和控制门口以及DMA控制器等。FU中MLU主要是用于机器学习算法的加速计算,而ALU应用于普通计算。
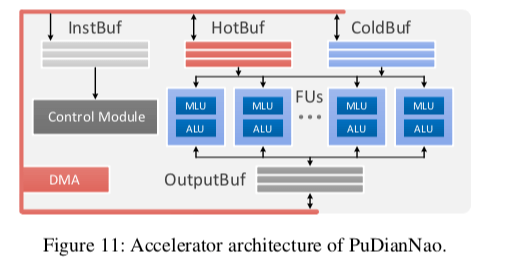
MLU中为一个六级的流水线(Counter, Adder, Multiplier, Adder tree, Acc, 和 Misc),当然不会所有个计算类似都会用到流水线的每一级。其中,Counter主要就是一个数,一个ACC有两个数据。ACC的输出会直接输出,而不会经过流水线。这里的用处是可以用于朴素贝叶斯、分类树等的计数操作。如果没有这类的操作,这一个stage会跳过;Adder执行向量加法运算;Multiplier则是向量乘法运算;Adder tree将多个Multiplier求和,和DianNao中的Adder Tree类似;Acc用于在一些情况喜爱部分结果的缓存;Misc实现一些非线性激活函数之类的功能。PuDianNao使用混合精度的设计,其中Adder、Multiplier和Adder tree使用16为复电,而其它的部分使用32为浮点。
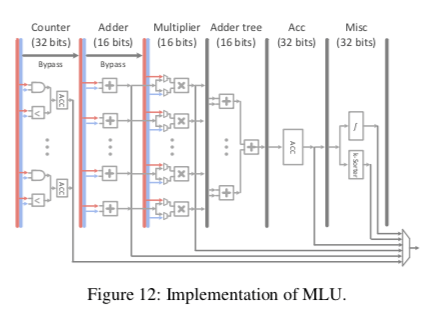
Buf设计采用了类似DianNao中的分离设计。另外控制门口使用了一些抽象的操作指令。指令这部分可以看看Cambricon的论文。
0x03 评估
这里的具体信息可以参看[1].
参看
- Tianshi Chen, Shijin Zhang, Shaoli Liu, Zidong Du, Tao Luo, Yuan Gao, Junjie Liu, Dongsheng Wang, Chengyong Wu, Ninghui Sun, Yunji Chen, and Olivier Temam. 2015. A small-footprint accelerator for large- scale neural networks. ACM Trans. Comput. Syst. 33, 2, Article 6 (May 2015), 27 pages. DOI: http://dx.doi.org/10.1145/2701417.
- DaDianNao: A Machine-Learning Supercomputer, MICRO ‘14.
- PuDianNao: A Polyvalent Machine Learning Accelerator,ASPLOS ’15.
- In-Datacenter Performance Analysis of a Tensor Processing Unit, ISCA ‘17.
