Split Block Bloom Filters

0x00 Block Bloom Filters

Block Bloom Filter是用了解决一般的Bloom Filter其Cache不友好的问题的。 Block Bloom Filter基本思路是将一个key要设置的bits都弄到一个block中，这个block一般根据cache line的大小来设计，比如一般的cache line大小为64bytes，512bit。Block Bloom Filter就可以看作是一个一般的Bloom Filters的一个数组，其添加/查询可以看作是现从Bloom Filters的数组里面找到一个Bloom Filters，然后设置这个Bloom Filters。这样就是Block Bloom Filters的第一个hash函数用于确定选择哪一个block，后面的hash函数用于选择一个block中的那些bits。其添加算法可以描述如下。

void block_insert(block b, uint x) 
  block masked = mask(x)
  int bits_num = sizeof x * 8
  for i in [0..7] 
    for j in [0..(bits_num-1)] 
      if (masked.getWord(i).isSet(j)) 
        b.getWord(i).setBit(j)

block mask(uint x) {
  block result
  for i in [0..7] 
    uint y = x * salt[i]
    result.getWord(i).setBit(y >> 27)
  return result

Block Bloom Filters单个block里面就是一个一般的Bloom Filter，所以其单个block的FPR计算和一般的一样。对于整体的FPR来说，Block Bloom Filters会比一般的Bloom Filters要高一些。在[2]中的计算结果，Block Bloom Filters的FPR为 \(f_{bloom}(B, c, k) = \sum_{i=0}^{\infin} Poisson_{B/c}(i)\cdot f_{inner}(B, i, k).\) 其中B为bits数量，i为一个block内元素的数量，k为hash函数的数量，c为平均为每个元素分配的bits数量。这里使用了泊松分布来作为二项分布的一个近似。Block Bloom Filter这样的设计实际上对于FPR来说是不利的。[2]中的数据说的是在c = 8bit，B = 512 bit的时候，Block Bloom Filter的FPR为0.0231, [1]中的说Block Bloom Filters实现1%的FPR时，同样的空间一般的Bloom Filter可以实现0.63%的FPR，[1]中选择的block长度为256bit，即 B = 256 bit。

0x02 Split Block Bloom Filters

Split Block Bloom Filters则是在Block Bloom Filters上面的一些优化。前面的 Block Bloom Filters使用的在一个blocks里面每个workd都设置一个bit的方式，而在这里使用avx2指令一次性计算8个hash(使用_mm256_mullo_epi32 rehash之后在取最高的5bits)，得到8个hash。然后将将一个ymm，即256长的一个寄存器当做8个32bit的整数，每个移动对应的位数。在与之前的做一个or，即完成设置。这个也是这里为什么选择256bit长的block的原因。[1]中给出的使用avx2指令的简单实现版本为：

// Takes a hash value and creates a mask with one bit set in each 32-bit lane. 
// These are the bits to set or check when accessing the block.
__m256i make_mask(uint64_t hash) {
  const __m256i ones = _mm256_set1_epi32(1);
  // Set eight odd constants for multiply-shift hashing
  const __m256i rehash = { INT64_C(0x47b6137b) << 32 | 0x44974d91,
                           INT64_C(0x8824ad5b) << 32 | 0xa2b7289d, 
                           INT64_C(0x705495c7) << 32 | 0x2df1424b, 
                           INT64_C(0x9efc4947) << 32 | 0x5c6bfb31};
  __m256i hash_data = _mm256_set1_epi32(hash);
  hash_data = _mm256_mullo_epi32(rehash, hash_data); 
  // Those five bits represent an index in [0, 31)
  hash_data = _mm256_srli_epi32(hash_data, 32 - 5); // reducing the hash values from 32 bits to five bits.
  return _mm256_sllv_epi32(ones, hash_data);
}
void add_hash(uint64_t hash, uint64_t num_buckets, __m256i filter[]) { 
  const uint64_t bucket_idx = block_index(hash, num_buckets);
  const __m256i mask = make_mask(hash);
  __m256i *bucket = &filter[bucket_idx];
  _mm256_store_si256(bucket, _mm256_or_si256(*bucket, mask));   // or the mask into the existing bucket
}

Xor Filters: Faster and Smaller Than Bloom and Cuckoo Filters

0x10 基本结构

这篇Paper提出了也是一个类似Bloom Filter一样在一定fast positive probability的情况下给出一个key是否存在一个集合中的一个回答。Xor Filters号称能够实现比Bloom Filter和Cuckoo Filter更快的速度和更好的空间。Xor Filters的基本思路是将一个key映射到k-bit的fingerprint，这样错误率就是1/2^k。其讲所有keys保存到一个k-bit fingerprint的数组B里面，这个数组B的大小略大于元素集合的大小|S|，c ≈ 1.23 × |S|。其想要实现在这个B上，对于存在的key，有(B[h0(x)] xor B[h1(x)] xor B[h2(x)] = fingerprint(x))成立，其中h0 h1 h2以及计算fingerprint的都是独立的hash函数。这样探测一个key是否存在就可以使用fingerprint(x) = B[h0(x)] xor B[h1(x)] xor B[h2(x)]来表示。后面就是如何构造这样的一个满足要求的数组B。其构造主要分为两个步骤，一个就是构造一个满足要求的映射，返回一个保存了这个映射消息的一个stack，然后就是将B数组对应位置上面赋值的操作。

Algorithm 2 Construction:
  Require: set of keys S Require: a fingerprint function
  repeat
    pick three hash functions h0, h1, h2 at random, independently from the fingerprint function 
  until map(S,h0,h1,h2) returns success with a stack σ (see Algorithm 3)
  
  B ← an array of size ⌊1.23 · |S|⌋ + 32 containing k-bit values (uninitialized) 
  assign(σ,B,h0,h1,h2) (see Algorithm 4)
  return the array B and the hash functions h0, h1, h2

Algorithm 3的核心是在B上面找到一个位置保存一个key的fingerprint，要求不能有两个key选择了同样的位置。另外一个要求是考虑到Algorithm 4赋值的操作是如下所示。Algorithm 4从顶到下遍历Algorithm 3得到的stack，并将对应的index赋予 fingerprint(x) xor B[h0(x)] xor B[h1(x)] xor B[h2(x)] 的值，这里这个 fingerprint(x) xor B[h0(x)] xor B[h1(x)] xor B[h2(x)] 其实就是B[h0(x)] xor B[h1(x)] xor B[h2(x)] 这三个位置值的xor。在保证正确性的要求下，其要求B[i]只能被写入一次，而且在写入[i]的时候被读取用于计算处理保存到B[i]的数值之后，其值也不能被修改。即B上一个位置只能修改一次，而且读取了之后就不能被写入。

Algorithm 4 Assigning Step (assign):
  Require: σ,target array for fingerprint data B,hash functions h0,h1,h2 
  for (x,i) in stack σ do
    B[i] ← 0
    B[i] ← fingerprint(x) xor B[h0(x)] xor B[h1(x)] xor B[h2(x)] 
  end for

Xor Filters用Algorithm 3实现这样的目标，其基本思路是对每个key，选择3个可能的位置，将所有可能映射的消息保存到一个set的数组H之后。在H中选择只有一个key映射到这个位置的，将i保存到一个队列Q，这样就能保证其只会有一次的写入。这个选择的位置i和key一起保存到stack中，被Algorithm 4使用。在一个key选定了一个位置之后，其会从H中移除。然后根据新的情况需要的时候添加到Q之中。这样的方式决定了一个操作的位置和顺序，保证B中一个index只会被写入一次，而且读取了之后不会被写入。只会被写入一次很显然满足。读取了之后不会被写入可以用反证法来证明：假设其在Algorithm 4中，一个index被读取了之后还会在写入，那么在mapping操作的时候，其可以选择这个index。这样会出现这个key x可以选择index，stack下面的key也可以选择index。这样对应到H中对应位置的set不会只有一个元素，从而stack下面的这个key不会选择这个index的写入位置，故矛盾。所以一个index被读取了之后不会写入。

Require: set of keys S, k-bit integer-valued hash functions h0,h1,h2.
  let c ← ⌊1.23 · |S|⌋ + 32
  H ← an array of size c containing a set of keys (values from S), initially empty 
  for all x in S do
    append x to H[h0(x)] 
    append x to H[h1(x)] 
    append x to H[h2(x)]
  end for
  Q ← initially empty queue 
  for i = 0 to |H | do
   if the set H[i] contains a single key then add i to Q endif 
  end for
  σ ← initially empty stack 
  while queue Q is not empty do
    remove an element i from the queue Q
    if the set H[i] contains a single key then
      let x be the sole value in the set H[i] push the pair (x,i) on the stack σ 
      for j = 0 to 2 do
        remove x from the set H[hj(x)]
        if the set H [h j (x )] contains a single key then add h j (x ) to Q endif 
      end for
    end if
 end while
 return success and the stack σ if |σ | = |S |, else return failure

Xor Filters的一个缺点是其构造的时候需要开辟一个与B等长的一个set的数组。另外其在两个元素/key出现了映射到三个同样的位置的时候，就无法处理，也就是说可能出现Algorithm 2的repeat操作，操作了很多次都无法映射成功。而且当构造的数据里面存在相同的元素的时候，这个总是会出现。

Stacked Filters: Learning to Filter by Structure

0x20 基本思路

Stacked Filters的基本思路是使用多层的filters堆叠而成， 所以称之为Stacked Filters。其基本思路是，对于false-positive的元素，其出现的频率也是不一样的。如果有一种方式，将false-positive中元素变成可以过滤，剩下的为出现频率不高。从FPR来说可能没有变化，但是从查询次数的角度，给出错误回答的次数会降低。之前这样的一些思路是learning的方法，即从过去的查询中学习。这里的思路就是如下图所示。

• 其层数从1开始，奇数层为记录元素集合中出现过的元素，而偶数层记录知道的频繁查询的没有出现过的一些元素。按照下图中最右边的查询示意图。其在对于L1层就可以reject的元素，就可以直接给出reject的回到。如果L1层不能reject，则到L2层查询。L2层是通过频繁查询的一些不在集合中元素构造而来，如果其给出肯定的回答，则其可能存在，也可能不存在，需要继续往下面查找。如果L2其给出了否定的回答，则其表面没有出现在最频繁查询而且不存在集合中的之中，则直接给出accept，认为其存在。这样的话，在L2层筛选之后，能够得到L3的，一般是频繁查询的不存在集合中的元素。L3就可以针对这些元素来进行针对性过滤，提高其FPR的表现。

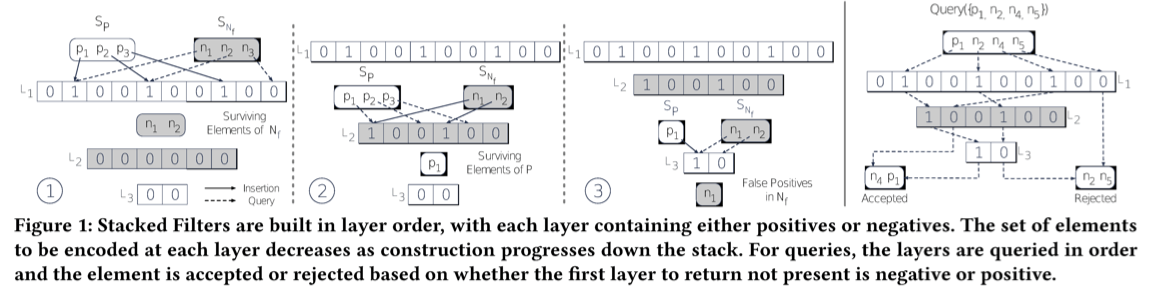
Stacked Filters其构造算法如下，构造是一个分层构造的过程。在构造的时候，需要知道数据集、worload的消息已经一些限制消息。其会根据一个优化算法给出那些认为是需要最早negative集合SN-f中记录的。然后后面分层构造的的时候，构造positive层的时候，记录在SN-f中存在但是给出错误回答哦的，这个会在下一negative层构造的时候被使用。构造negative层时候，也会有类似的一个操作。

这篇Paper后面还有很对的关于对Stacked Filters的FPR，以及优化，如何实现adaptive的一些分析。其风格也符合这篇paper作者之前的一些论文，比较多的数学推导。

参考

1. Split block Bloom filters, arXiv.
2. Cache-, Hash- and Space-Efficient Bloom Filters.
3. Xor Filters: Faster and Smaller Than Bloom and Cuckoo Filters, arXiv.
4. Stacked Filters: Learning to Filter by Structure, PVLDB ‘21.