Start-Time-, Multi-Queue-, Device-Direct- Fair-Queuing

Start-Time Fair Queueing and Its’ Variants

0x00 Start-Time Fair Queueing

Fair Queuing是一种常见的QoS、调度的方法。以Weighted Fair Queuing为例，其会为每个请求附加上两个tags，stat tag和finish tag。两个tags按照如下的方式定义： $定义p_f^j, l_f^j分为flow\ f的第j个packet和这个packet的长度.\\ 则S(p_f^j) = \max\{v[A(p_f^j)], F(p_f^{j-1})\}, j \geq 1 \\ F(p_f^j) = S(p_f^j) + \frac{l_f^j}{\phi_f}, j \geq 1. \\ 另外F(p_f^0) = 0, v(t)定义为 \frac{dv(t)}{dt} = \frac{C}{\sum_{j \in B(t)}{\phi_j}}. \\$ C为服务的整体容量，B(t)为backlogged flows的集合，即有要调度packets的flows的集合。调度的时候按照finish tag的升序调度。WFQ的一个问题就是v(t)的计算问题。Start-Time Fair Queueing在paper[1]中提出。SFQ算法改了v(t)的定义，其同样有start-tag和finish-tag，定义如下: $S(p_f^j) = \max\{v(A(p_f^j)), F(p_f^{j-1})\}, j \geq 1.\\ F(p_f^j) = S(p_f^j) + \frac{c_f^j}{\phi_f}, j \geq 1, and\ F(p_f^0) = 0. \\$ 和WFQ不同,调度的时候是根据start-tag的升序来调度。初始的时候virtual time设置为0，即v(0) = 0，其余时候定义v(t)如下：

During a busy period, the server virtual time at time t, v(t), is defined to be equal to the start tag of the packet in service at time t. At the end of a busy period, v(t) is set to the maximum of finish tag assigned to any packets that have been serviced by then.
Observe that server virtual time changes only when a packet finishes service. Also, we set v(t) to the maximum of the finish tags of the packets at the end of busy period only for clarity of proofs; all the start tags as well as the server virtual time can be equivalently set to zero

SFQ的fairness能满足: $|\frac{W_f(t_1, t_2)}{\phi_f} - \frac{W_m(t_1, t_2)}{\phi_m}| \leq \frac{l_f^{max}}{\phi_f} + \frac{l_m^{max}}{\phi_m}.\\$ 其证明可以参考论文[1].

0x01 Min-SFQ, Max-SFQ, 4-Tag SFQ

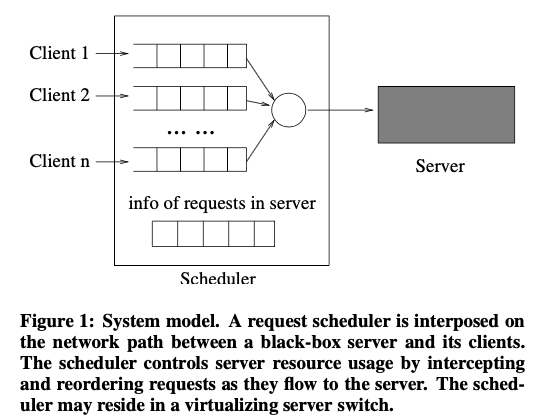
在Paper中提出了SFQ的几个变体，其先分析了初始版本的SFQ存在的一些问题(在paper[2]面向的环境下，如下图的模型)。在paper[3]中，也简要的分析了Min-SFQ, Max-SFQ, 4-Tag SFQ几种SFQ的变体：

Min-SFQ(D)，其中D指的是在如下的模型中，将outstanding的请求控制到数量D。Min-SFQ(D)算法中，v(t)总是为outstanding请求(已经dispatched了但是还没有completed的请求)中最小的start-tag。这样的一个问题是vritual time可能推进得太慢，导致一些unfairness。比如一个flow f在上其前一个请求要完成之前就提交了下一个请求，因为f有outstanding的请求，则 $v(t) \leq S(p_f^j), and\ S(p_f^{j+1}) = S(p_f^j) + \frac{c_f^j}{\phi_j}$ 即目前的stag-tag和上个请求的finish-tag对应。因为这里设置为outstanding最小的，那些推进更快，更aggressive的start-tag也不会对这个造成影响。而这样就是根据flow f请求达到的速度推进的。然后有的flow更加aggressive的话，这个flow f就获取不到其应该可以获取到的资源份额。
Max-SFQ(D)/SFG(D)/Min-SFQ类似于推进virtual time是根据lagging flows而来。另外的一种方式是根据backlogged flows而来。一种方式是v(t)根据正在排队的请求而来，而不是已经dispatched的请求。如果一个请求在一个flow的下一个请求达到之前被dispatched，v(t)同样会被推进，而不是被lagging的影响。这个思路可以进一步改动一下，将v(t)定义为在时间t or t之前dispatched的最后的请求的start-tag，在[3]中也将SFQ(D)称之为Max-SFQ(D)，因为Max-SFQ(D)算法则是将v(t)总是设置为outstanding请求中最大的start-tag。这样可能导致的问题就是virtual time推进得太快；
4-Tag SFQ(D)，4-Tag SFQ(D)在前面两种SFQ变体算法的基础上继续改进，它维护了两组的tag，一组为SFQ对应的tags。另外一组称之为adjusted start tag，类似于Min-SFQ(Q)中的方法来打这个tags。virtual time也对应两个，一个 virtual time, 另外一个称之为adjusted virtual time。v(t)根据最后一个dispatched的请求的start-tag来定义，而adjusted virtual time根据请求中最小的start-tag来定义： $如果F(p_f^{j-1}) < v(t), 则 \bar S(p_f^j) = \max\{\bar v(A(p_f^j)), F(p_f^{j-1})\}, 否则有 \bar S(p_f^j) = \max\{\bar v(A(p_f^j)), \bar F(p_f^{j-1})\}; \\ 另外有 \bar F(p_f^{j-1})\} = \bar S(p_f^j) + \frac{c_f^j}{\phi_f}; S(p_f^j) = \max\{v(A(p_f^j)), \bar S(p_f^{j})\}; F(p_f^{j-1})\} = S(p_f^j) + \frac{c_f^j}{\phi_f}; \\$ $\bar S(p_j^f)$即为adjusted start tag，其它同理。0时刻，Finish tags都定义为0，virtual time也都定义为0。这里设置tags的时候，先判断上一个请求的finish tag和目前v(t)的比较。如果小于，即有另外flow的请求在以一个比这个finish tag大的start tag dispatched了，而且请求没有完成。按照原来SFQ的方式，会直接设置为v(t)，但是这里可能v(t)或者是adjusted start tag，可能获得一个extra credits。调度的时候还是根据S来调度。。另外关于两个virtual time的定义：
```
Initially v(t) and v¯(t) are both 0. During a busy period, v(t) is defined as the start tag of the last dispatched request. v¯(t) is defined as the minimum start tag of all outstanding requests. At the end of a busy period, v(t) and v¯(t) are set to the maximum finish tag assigned to any request that has been serviced by time .
```

Multi-Queue Fair Queuing

0x10 基本思路

Fair Queuing的一个问题是使用一个中心的队列，这种在一些并发冲突比较多的情况下，会对性能有比较大的影响。Multi-Queue Fair Queuing的思路是讲一个中心的队列改成per-CPU的多个队列。这样降低并发冲突之外，带来的问题是如果实现队列之间的同步问题，以及保持原来的Fair Queueding算法的逻辑。为了处理不同队列之间的imbalance的问题，MQFQ会限制最快的队列比最慢的队列能够领先的幅度。如果这个阈值T设置为0，可能最大地保持Fairness，但是会影响性能。所以这里的一个问题就是如何设置这个阈值T。

MQFQ由于有多个queue，这样不但完成时间是是out of order的，dispatched时间也会是out of order的。这里定义一个 per-flow virtual time ，另外讲处理对于那些请求已经submitted，但是还没有dispatched到devcie的flow，定义为 lagging flow。Per-flow virtual time处理这些flows不会积累资源到后面使用。一个flow f的vt定义为最老的一个已经submitted但是还没有dispatch的请求的start tag。如果一个flow有多个等待dispatch的请求，则dispatch这个最老的请求的时候，会导致这个f增加virtaul time值l/r。其中r为这个f 的weifht，而l为请求的size。同时定义为global virtaul time为所有per-flow virtaul time中最小的。
请求处理的时候，根据根据start tag的顺序来进行处理。一个flow lagging的时候，它不在多global virtaul time VT造成影响。这里因为一个请求R的start定义为VT和per-flow end tag的最大值，end tag定义为R的start加上预期的服务时间。而VT有定义为per-flow VT的最小值。如果lagging的时候(lagging flow (i.e., a flow that is not backlogged。这个的意思里应该是没有新来的请求了))，这样导致的一个效果就是这个flow的start tag还是are still subject to the lower bound of current virtual time。start tag的计算：
```
on submission of request R:
  set R’s start tag = MAX(VT, per-flow end tag) 
  set R’s end tag = R’s start tag + R’s service time 
  update per-flow end tag
  insert R in local queue
  if R goes at the head
    update VT 
  dispatch()
```
MQFS的处理方式是限制超出start tag超过VT阈值T的请求被dispatched。限制的方式是通过限制head为flow f的请求的队列。限制了head之后，因为请求根据start tag排序，后面的请求就会同样被限制。这样就可可以避免一个flow超出太多。

MQFQ dispatch请求的基本逻辑：

dispatch():
  if local queue is in throttling wheel
    remove it from wheel
  if local queue is in ready queues
    remove it from ready queues 
  if local queue is empty
    return
  for lead request R from local queue
    if R’s start tag is more than T ahead of VT 
      add local queue to throttling wheel 
      return
    attempt to obtain slot from token tree 
    if unsuccessful
      add local queue to set of ready queues
      return
    remove R from local queue deliver R to device 
    update VT
    if VT has advanced a bucket’s worth
      turn the throttling wheel
      unblock any no-longer-throttled queues 
        for which slots are readily available
      add the rest to the set of ready queues

MQFQ的fiarness相比于一个中心队列的有所不同，要地一些，paper中有数据分析。

0x11 Scalability

这里描述了一些MQFQ为性能优化的一些设计。在MQFQ中，一个flow有lagging变成backlogged，即有没有积压的请求变成有的时候，请求的start tag设置为当前的VT，请求不停增加的时候，这个start tag就是一直增长的，这种情况的后面请求的start设置为前面请求的end tag，而VT还是所有队列中请求中最小的stag tag。计算全局的virtual time，VT，可以通过扫描所有的queue，这样简单但是效率太低。这里使用的方法为一个mindicator structure 的结构。这个结构为一个tree结构，其leaf node为queue，父节点为两个子节点的最小值。

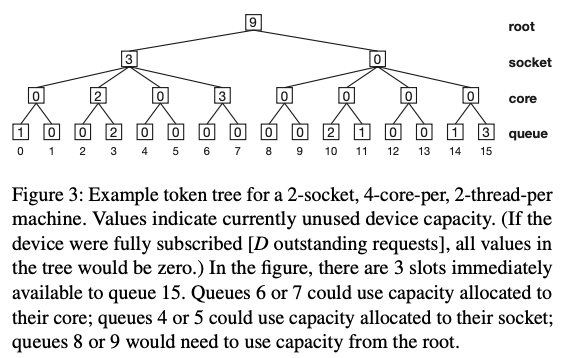
另外MQFQ需要追中每个设计资源的使用情况，有些请求在处理中还没有完成的。这里使用上图的结构，也是一个树形的结构。其中的值表示剩余资源的量，父节点表示分配给这层面的剩余的资源的来。这里就是一个multi layer的资源分配的方式。最底层的为queue，上面为core、socket。root为全局的剩余。如果一个queue的资源使用完了，会尝试从上一层的获取剩余的资源，以此类推。到最上层还没有的话就是申请不到，但是在其它的节点可能还是有剩余的资源。想要一种向上传递的机制。在资源释放的时候，释放到local and the target CPU的最小公共祖先这一层。

参考

Start-Time Fair Queueing: A Scheduling Algorithm for Integrated Services Packet Switching Networks. Transaction on Networks ‘97.
Interposed Proportional Sharing for a Storage Service Utility, SIGMET ‘04
FlashFQ: A Fair Queueing I/O Scheduler for Flash-Based SSDs, ATC ‘13.
Multi-Queue Fair Queuing, ATC ‘19.
D2FQ: Device-Direct Fair Queueing for NVMe SSDs, FAST ‘21.